Анықталған интеграл және оның қасиеттері

Шымкент аграрлық колледжі
Бедебаева Айгуль Ерсултановна

Дәрістің тақырыбы: «Анықталған интеграл және оның қасиеттері»

Дәрістің мақсаты

Білімділік: Оқушыларға анықталған интеграл ұғымы мен қасиеттерін және интегралды есептеу үшін Ньютон-Лейбниц формуласын қолдану бойынша білік, дағдыларын қалыптастыра отырып, білімдерін нақтылау.

Дамытушылық: интегралдарды есептеу кестелерін есте сақтау және оларды есептер шығаруда қолдана білуге дағдыландыру, логикалық ойлау қабілетін дамыту;

Тәрбиелік: Соңғы нәтижеге жету жолында табандылық пен жігерлілік көрсете білуге, өзін-өзі бағалай білуге тәрбиелеу.

Дәрістің түрі: Жаңа сабақты меңгерту

Оқыту әдісі: Түсіндіру, сұрақ-жауап, жүйелеу, есеп шығарту

Әдістемелік қамтамасыз етілуі:

Көрнекіліктер: Таратпа материалдары, слайдтар, плакаттар.

ОТҚ: Интерактивті тақта

Пән аралық байланыс: Физика, информатика

Қолданылатын әдебиеттер:

1. Негізгі

1.Ә.Н.Шыныбеков. Алгебра және анализ бастамалары. 11-сыныпқа арналған оқулық.Алматы «Атамұра» 2007ж

2.А.Әбілқасымова Алгебра және анализ бастамалары  11  Алматы «Мектеп»  2007ж.

2. Қосымша

1. П.Т.Апанасов, М.И.Орлов Сборник задач по математике  Москва 1987г.

2. Н.В.Богомолов. Практические занятия по математике. Москва «Высшая школа» 1990г.

Дәрістің құрылымы мен мазмұны

І. Ұйымдастыру кезеңі:

1. Оқушыларды түгелдеу, дәрісхана тазалығын тексеру, оқушылардың сабаққа дайындығын бақылай отырып, зейінін сабаққа аудару.

2. Өткен білімдерге сүйене отырып, оқу әрекетін дамыту

ІІ. Үй тапсырмасын сұрау: Интегралдарды есептеудің негізгі әдістері.

"Есіңде ме, формула" – үй тапсырмасын қайталау, сұрақ-жауап

1. Тікелей интегралдау әдісі дегеніміз не?(5 ұпай)

Тікелей интегралдау әдісі дегеніміз берілген интегралды ешқандай әдістерді қолданбай тікелей интегралдау формуласына салып шығару.

2. Айнымалы ауыстыру әдісі дегеніміз не?Мысал келтір.  (10 ұпай)

3. Қандай интегралдық есептерде бөліктеп интегралдау әдісін қолданамыз?   (15 ұпай)

     Көбейтінді түрде берілген екі функцияны интегралдауда қолданамыз.

    

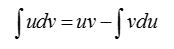
4. хⁿ-ның интегралы  (5 ұпай)

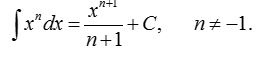
5.aⁿ-ның интегралы  (10 ұпай)

6. 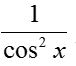  -тың интегралы  (15 ұпай)

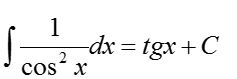
7. Анықталмаған интеграл дегеніміз не?  (5 ұпай)

Анықтама: Берілген аралықтағы F(х) функциясының алғашқы функциясы осы аралықтағы f(х) функциясының анықталмаған интегралы деп аталады.

Белгіленуі: 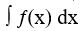икстен эф де икс функциясының анықталмаған интегралы деп оқылады)

Анықтамаға сәйкес: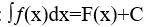

Мұндағы: 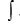   - интеграл таңбасы

                  f(х) – интеграл астындағы функция

                  f(х) dx – интеграл астындағы өрнек

                  х- интегралдау айнымалысы

                  C- кез-келген тұрақты шама

8. Интегралдау ережелері: (10 ұпай)

      

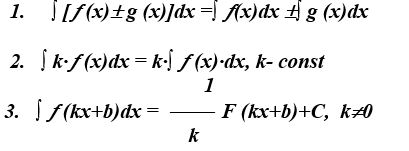
9. Анықталмаған интеграл қасиеттері: (15 ұпай)

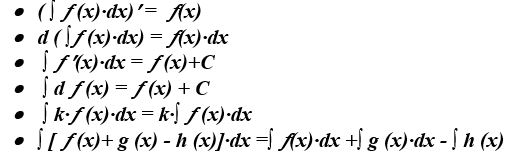
"Қатесін тап" ойыны- үй тапсырмасын қайталау  (3 ұпай)

 

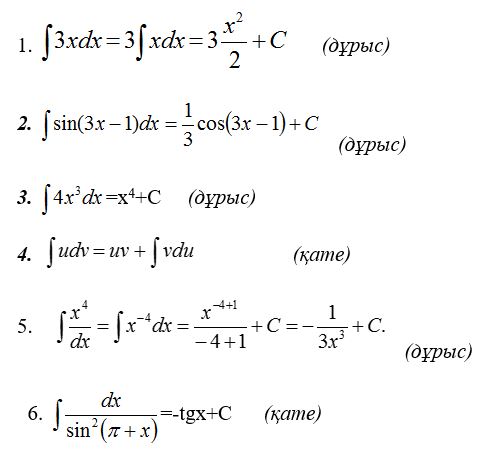
ІІІ. Жаңа сабақ:

 

Жаңа сабақтың жоспары

1.    Анықталған интеграл қасиеттері
2.    Ньютон-Лейбниц формуласы
3.    Мысалдар келтіру
4.    «Жасырын суретті анықтау»
5.    «Сиқырлы сандықша»
6.    Қорытынды: оқушыларды үй тапсырмасына және жаңа сабаққа қатысуы барысында алған ұпайлары бойынша бағалау.

Жаңа материалды түсіндіру.

1. F(b) - F(a) айырмасын y=f(x) функциясының [a;b] кесіндісіндегі анықталған интегралы деп атайды.

Мұндағы a және b сандары интегралдау шектері: a – төменгі шегі,  ал b – жоғарғы шегі.

Анықталған интегралдың негiзгi қасиеттерi.

Берiлген анықталған интегралдың бар болу шарты орындалады деп есептейiк.

1⁰. Тұрақты санды анықталған интеграл белгiсiнiң алдына шығаруға болады:

                        ,

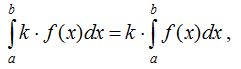мұнда k=const .

2⁰. Бiрнеше функциялар қосындысының анықталған интегралы қосылғыштарының анықталған интегралдарының қосындысына тең:

      .

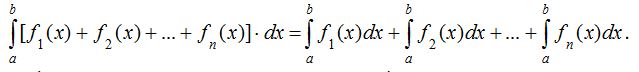Осы екi қасиет интегралдың сызықтық қасиетi деп аталады.

3⁰. Егер [a;b] аралығын [a;c]  және [c;b] аралықтарына бөлсек, онда

                                

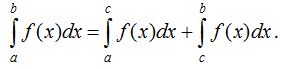
4⁰. Егер интегралдың жоғарғы шегi мен төменгi шегiнiң орындарын ауыстырсақ, онда оның таңбасы өзгередi:

                            

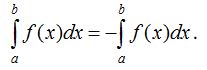
5⁰. Жоғарғы шегi мен төменгi шегi тең болатын интеграл 0-ге тең

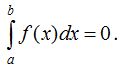
6⁰. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi үшiн болса, онда

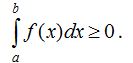
7⁰. Егер [a;b]  аралығындағы х айнымалысының барлық мәндерi үшiн 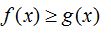 болса, онда

                               .

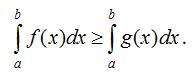8⁰. Егер [a;b]  аралығында функциясының ең үлкен және ең кiшi мәндерi сәйкес М және m сандары болса, онда

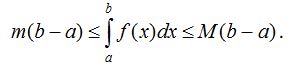
2. Ньютон-Лейбниц формуласы.

Ньютон Исаак (1643-1727) - ағылшын астрономы, физигі, әрі  математигі. ХVII ғасырда дифференциалдық және интегралдық есептеулерді математикалық практикаға енгізді.

Туындыны дифференциалдау деп атаған және  интеграл белгісін енгізген Лейбниц

Готфрид Вильгельм Лейбниц (1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де жан-жақты дамыған философ. Екінші жағынан, ол - математик, физик, саясаткер, тарихшы, құқықтанушы.

Теорема. Егер F(X) функциясы [a;b]  аралығына f(x) функциясының алғашқы функциясының бiрi болса, онда

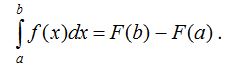        (5)

Бұл теңдiк Ньютон-Лейбниц формуласы деп аталады.

Анықталған интегралдарға байланысты мысалдар келтіру.

1-есеп. .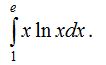

Интеграл астындағы функцияның алғашқы функциясын бөлiктеп интегралдау әдiсiмен тауып және оған Ньютон-Лейбниц  формуласын қолдансақ,

           

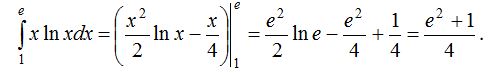
2-есеп. .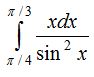

Бөліктеп интегралдау формуласы бойынша 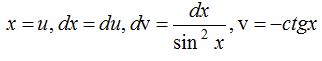 болса, онда

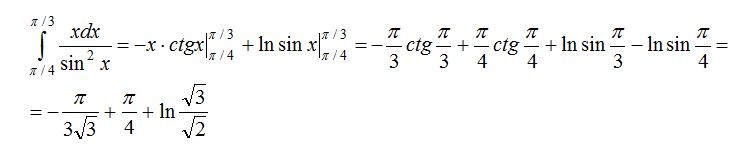
3-есеп.                                       

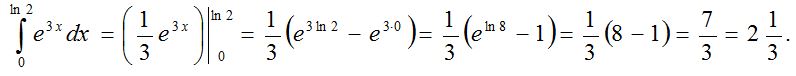
4-есеп.

 

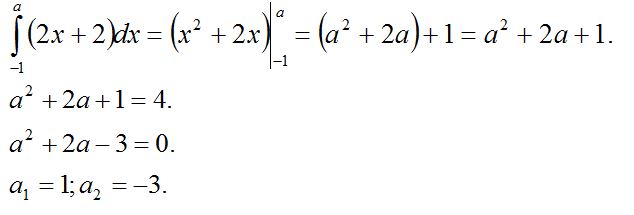
ІV. Жаңа сабақты бекіту: "Жасырын суретті анықта " ойыны  (ұяшықтарға жасырылған есептерді шығару арқылы, астындағы суретте кім бейнеленгенін анықтау қажет)

 

Лайықтап жазылған ұпайлары,

Интегралға есеп бар мұнда тағы Алғашқы функциясын табарсың, қателеспей,

Жетерлік болса егер білім жағы.

 

"Сиқырлы сандықша" (сандықша ішіндегі есептерді шығару)

 

Үйге тапсырма

“Алгебра және анализ бастамалары, 11 сынып, А.Е.Әбілқасымова, 23-24 бет”

1. №42,43 (1,4)     

Бағалау парағы

Есіңде ме формула	Ойлан тап!	Жасырын суретті анықтау	Сиқырлы сандықша	Жалпы ұпайы

Бағалау ұпайлары

6-10 ұпай жинаған оқушылар 3 деген бағамен бағаланады

11-20 ұпай жинаған оқушылар 4 деген бағамен бағаланады

20 ұпайдан жоғары жинаған оқушылар 5 деген бағамен бағаланады.

---