Сандар дүниесіне саяхат
«№ 21 жалпы орта білім беретін мектебі» КММ-сінің
7 "ә" сынып оқушысы: Төрежанов Нұртілеу Нұркенұлы
Секция: Математика
Ғылыми жобаның жетекшісі: математика
пәнінің мұғалімі: Салықбаева Бану Жукеновна
Жезқазған қаласы 2016 жыл
Мазмұны
Аннотация ............................................................................................3
І. Кіріспе .............................................................................................4-5
ІІ. Негізгі бөлім:
1. Сиқырлы шаршыдағы сандар.............................................................6-7
2. «Баспалдақты шаршыдағы сандар»....................................................8
ІІІ. Қорытынды.......................................................................................16
ІV. Пайдаланған әдебиеттер .................................................................17
Аннотация
Жұмыс 1-ден 100-ге дейінгі натурал сандардың жүз торлы шаршыда орналасқаның зерттеу. Жүз торлы шаршылардың ішінен кез-келген өзі қалаған реттегі бір шаршыны таңдап алып, сол шаршыдағы сандардың қосындысын белгілі бір өрнек шығатындай есептегенде бір ғана қосындыға тең болатынын көрсете білу.
Кіріспе
«Нұрлы жол – болашаққа бастар жол» Қазақстан Республикасының президенті Н.Ә.Назарбаевтың Қазақстан халқына жолдауында : «Біздің болашаққа барар жолымыз Қазақстандықтардың әлеуетін ашатын жаңа мүмкіндіктер жасауға байланысты. ХХІ ғасырдағы дамыған ел дегеніміз – белсенді, білімді және денсаулығы мықты азаматтар. Барлық дамыған елдердің сапалы бірегей білім беру жүйесі бар. Оларға заманауи бағдарламалар мен оқыту әдістемелерін,білікті мамандар ұсыну маңызды. Оларды оқыту нәтижесі оқушылардың сындарлы ойлау, өзіндік ізденіс пен ақпаратты терең талдау машығын игеру болуға тиіс». Қазіргі заманғы білім берудің перспективалық міндеті – ол сындарлы ойлай білетін және ақпараттар ағынында бағдар ала білуге қабілетті адамдарды даярлау. Орта білім белсенді, білімді және табыстарға бағдарланған тұлғаларды тәрбиелеуге жауап береді. Оқушылар «ешқашан бастауды тоқтатпа, ешқашан тоқтауды бастама» деген ақиқаттан адаспауы тиіс .Математикалық ұғымдар, аксиомалар мен анықтамалар және қорытындылар (теоремалар және салдарлар) нақтылы өмірде бар болатын әртүрлі заттардың, онда болып жатқан құбылыстар мен өтіп жатқан процестердің өздеріне тән жалпы қасиеттерінің біздің санамызда бейнеленуі болып табылады. Академик А.Н. Колмогоров: «Математик әрқашан реалды құбылыстардың әртүрлі модельдерімен жұмыс жасайды. Оны, математик ретінде, қабылданған модель аясында қорытындылар орынды ма деген сұрақ ғана ойландырады. Егер де ол реалдылық пен оның математикалық моделінің арасындағы диалектикалық байланысты түсіндіру міндетінен бас тартса, бұл әсте жақсы емес» - деп көрсеткен болатын .
Зерттеу мақсаты. Жұмыс1-ден 100-ге дейінгі натурал сандардың жүз торлы шаршыда орналасқаның зерттеу. Жүз торлы шаршылардың ішінен кез-келген өзі қалаған реттегі бір шаршыны таңдап алып, сол шаршыдағы сандардың қосындысын белгілі бір өрнек шығатындай есептегенде бір ғана қосындыға тең болатынын көрсете білу.
Зерттеу міндеті. Шаршыларды сандардың қасиеттерін зерттеу арқылы математикалық білімді нақтылы меңгеру.
Тақырыптың өзектілігі. Зерттеу жұмысында шаршыдағы сандардың бір заңдылықтарын зерттей білу. Хабарланып отырған материалға тарихи бағдар беру, ілімнің практикалық мәнін ашып көрсету.
Зерттеудің болжамы. Оқу материалдарын игеру барысында зерттеу әдісін жетілдіріп, деректерді тиімді әрі жүйелі пайдалансақ, онда оқушылардың зерттеу құзіреттілігі және коммуникативтік, ақпараттық құзіреттілігі өз мәнінде дамып, сонымен қоса оқушылардың математикаға деген қызығушылығы артады деген ойдамын.
Зерттеу кезеңдері. Мен өзімнің ғылыми жұмысымды 4 кезеңге бөлдім.
І кезең: тақырыпты таңдау.
ІІ кезең: тақырыпқа байланысты тарихи, математикалық шығармаларды жинап оны топтау.
ІІІ кезең: табылған ақпаратты талдау және өңдеу.
ІV кезең: жұмысты жазып, қорғау.
Зерттеу құралдары. Зерттеу құралдары: математикалық кітаптар, бұқаралық ақпарат,интернет желісі.
Зерттеу әдісі: Анализ, синтез, жобалау әдісі.
Сандар дүниесіне саяхат
Натурал сандардың бірталай қасиеттерін ежелгі грек математиктері тағайындаған .Бізге жеткен аңыз бойынша Пифагор мен оның шәкірттері сандарды жұп және тақ , жай және құрама сандар деп топтарға бөлген. Алайда пифагоршылар, арифметикаға елеулі жаңалықтар енгізе отырып, сандардың табиғатын қате түсінген. Олар еш бір дәлелсіз, негізсіз «бір - ақылдың немесе сананың белгісі, бес - махаббаттың белгісі. 666 - айуандықтың белгісі» т.с.с деп, былшыл уағыздар таратқан. Бұл уағыздар беретін әр түрлі сұмпайылар мен балгерлердің қарта ашу, құмалақ тарту, сәуегейлік жасау сияқты әрекеттеріне арқау болған.
Орта ғасырлар математикасында «керемет «квадраттар»елеулі орын алған. Жолдарындағы, бағандағыларды және үлкен диагональдарындағы сандардың қосындылары өз ара тең болып отыратын квадрат таблица керемет квадрат деп аталып кеткен (орыс тілінде «магический квадраты», мұндағы «магический» сөзі араб тілінің «маги» сөзінен шыққан, мағынасы –«сиқыр»)
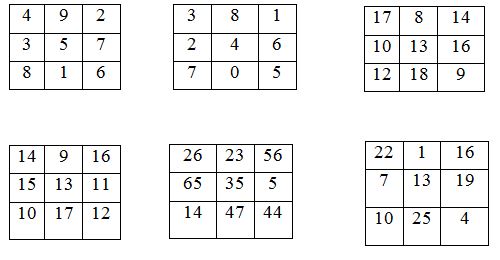
Үш жолды квардаттар
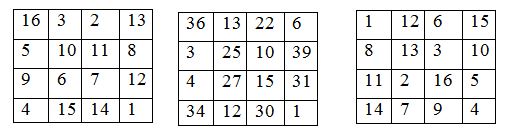
Төрт жолды квадраттар
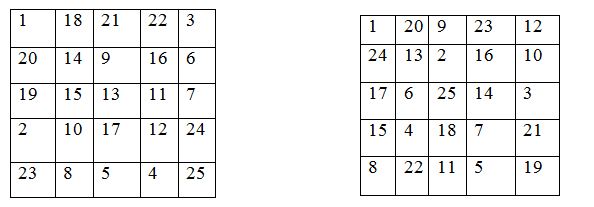
Бес жолды квадраттар
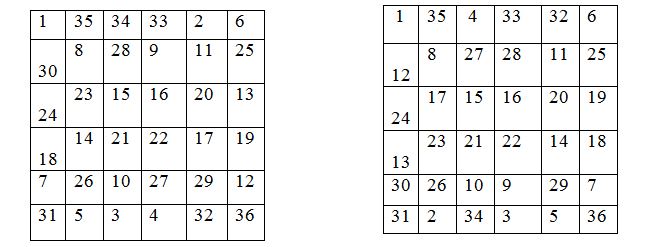
Алты жолды квадраттар
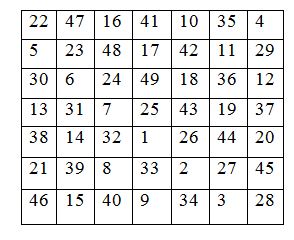
Жеті жолды квадрат
Баспалдақты квадрат
Жолының саны артқан сайын керемет квадратты құрастыру жұмысы қиындай береді. Соңғы жеті жолды квадраттың құрастырылуына тоқтай кетейік. Бір «диагоналы» верикаль орналасқан «баспалдақты квадрат» аламаз (181-б). Оның сатыларына, арадан бір бос орын қалдырып отырып ,1, 2, 3,...,49 сандарын жазамыз. Содан сон төбелері 46, 22, 4, 28 сандары бойынша анықталатын квадыраттын негіз етіп алып, оның бос орындарын әлгі квадыраттың сыртындағы сандармен толтырамыз. Атап айтканда 22 мен 16 арасындағы бос орынға 41-ді,10 мен 4 арасындағы орынға 35-ді т.с.с жазамыз. Басқа квадыраттарға да осы тәсілді қолдануға болады. Француз әуескойы Френикль де Бесси (1602-1775) төрт жолды керемет квадыраттардың жалпы саны 880 болатындығын тағайындаған және солардың бәрін құрастырып шыққан. 1640 жылы Ферма 14 жолды квадратты құрастырған. Кейбір математиктер керемет квадыраттарды кілен жай сандардан құрастыру жолдарын зерттеген 181 беттегі үш жолды квадыраттың әр жолындағы жай сандардың қосындысы 1077, төрт жолды квадыратта ондай қосынды 798-ге тең.
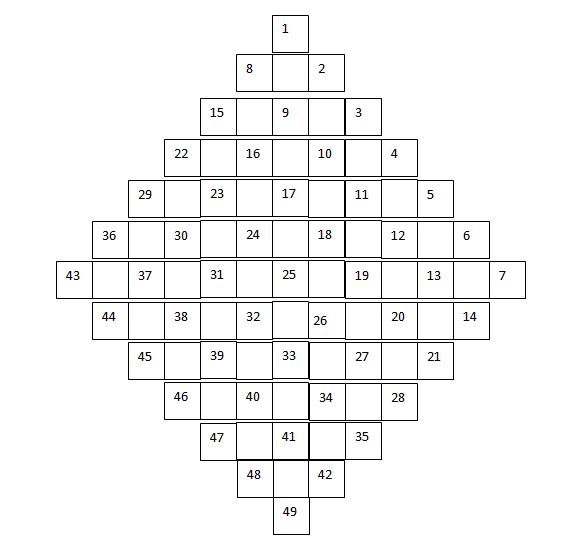
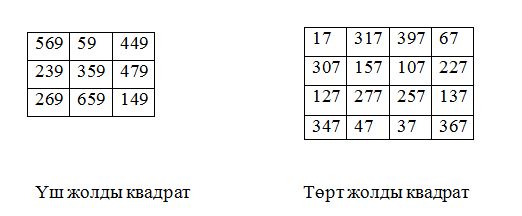
Қазақ тілінде керемет шаршылар жөнінде ешқандай мағұлматтар жоқтығы ескеріліп, төменде көп жолды шаршылардың кейбір үлгілері келтірілген.
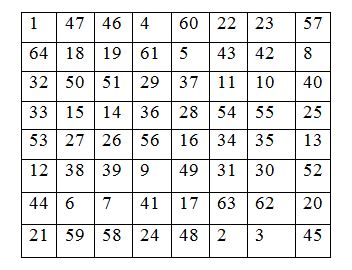
Сегіз жолды квадрат
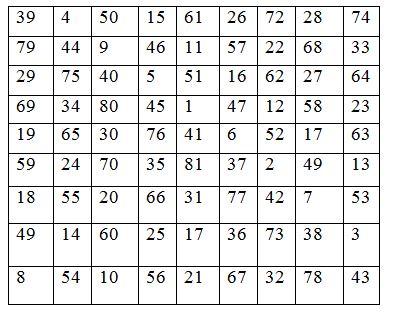
Тоғыз жолды квадрат
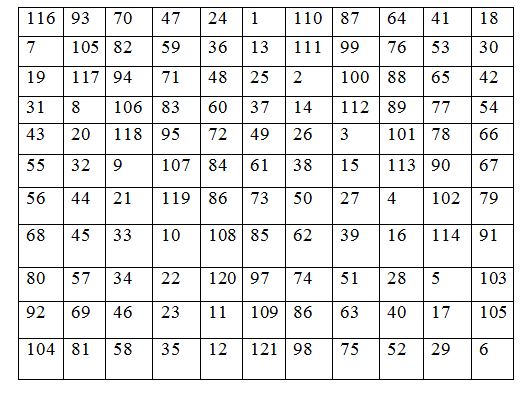
Он бір жолды квадрат
Ерте кезде кейбіреулер мұндай керемет шаршыларды ермек еткен, айтыс, жарыстарында пайдаланған, ал матеметиктер олардағы сандардың орналасу зандылығын зерттеген.
Керемет шаршылар мәселесімен орыс ғалымдарынан профессор В.П. Ермеков, академик Я.В. Успенский т.б.шұғылданған. Олардың еңбектері жөніндегі және еремет квадыраттар теориясының әлі шешілмеген жұмбақтары жөніндегі деректоры М.М.Постниковтың «Керемет квадраттар» атты кітапшасынаноқып алуға болады (Мәскеу,1964).
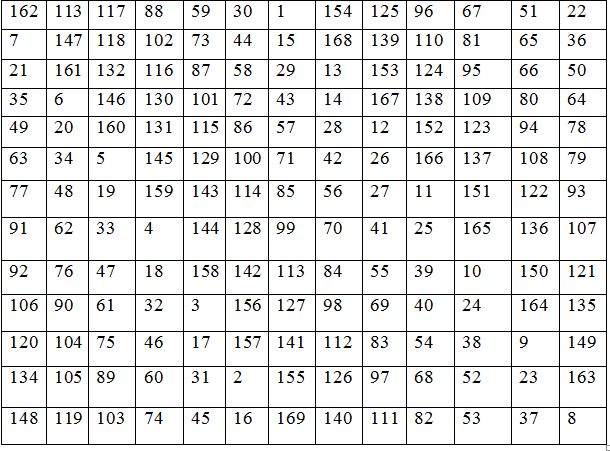
Он үш жолды квадрат
Кейбір сандардың қосындысы мен көбейтіндісі бірдей цифрлармен жазылып шығады, бірақ цифрлардың орнындары ауысқан болады. Мысалы:
9+9 =18, 9*9=81,
24+3=27, 24*3=72,
47+2=49, 47*2=94,
263+2=265, 263*2=526,
497+2=499, 497*2=994.
Кейбір екі таңбалы сандардың көбейтіндісіне көбейткіштердің цифрларын ауыстырып жазуға болады. Одан көбейтіндінің шамасы өзгермейді:
12*42=21*24, 12*63=21*36,
12*84=21*48, 13*62=31*26,
23*96=32*69, 24*63=42*36,
24*84=42*48, 26*93=62*39,
36*84=63*48, 46*96=64*69.
Кейбір сандардың шаршлары тетелес екі сан арқылы жазылады:
912=8281, 90792=82 428 241,
99012=98 029 801,
88 225 2952=7783 702 677 837 025,
99 990 0012=9998 000 299 980 001.
Бұларда тетелес екі санның үлкені сол жақта, кішісі оң жақта орналасқан. Кішісі сол жақта, үлкені оң жақта орналастындары да бар:
4282=183 184, 8462=715 716,
78102=60 996 100, 36 3652= 1322 413 225,
63 6362=4049 540 496 т.с.с
Шаршылары бір санның қайталануы арқылы жазылатын сандар да аз емес:
36 363 636 3642=1322 314 049 613 223 140 496
63 636 363 6372=4049 586 776 940 495 867 769
90 909 090 9102=8264 462 810 082 644 628 100
Бұл сияқты сандардың бір сыпырасы Б.А. Кордемскийдің кітабында келтірілген. Сандардың кубтарында да әр түрлі қызық қасиеттер бар. Мәселен:
13=1,
13+23+33=(1+2+3)2,
13+23+33+43=(1+2+3+4)2,
13+23+33+43+53=(1+2+3+4+5)2.
142 857 санын бірден бастап жетіге дейінгі сандарға көбейтейік. Сонда мынадай сандар шығады:
142 857*1=142 857,
142 857*2=285 714,
142 857*3=428 571
142 857*4=571 428,
142 857*5=714 285,
142 857 6=857 142,
142 857*7=999 999.
Мұның алдыңғы алтауы алғашқы алынған санның цифрларын сол жағынан оң жағына көшіру арқылы жасалып отыр. Соңғысының цифрлары – кілең тоғыздықтар. 0 588 235 294 117 647 саны да осындай. Шынында да:
0 588 235 294 117 647*1=0 588 235 294 117 647,
0 588 235 294 117 647*2=1 176 470 588 235 294,
0 588 235 294 117 647*17=9 999 999 999 999 999.
Цифрлардың осы сияқты айналып келу қасиеті 052 631 578 947 368 421 санында да байқалады.
Бірінші санда 6, екіншіде 16, үшіншіде 18 цифр бар. Периодты бөлшектің бәрінен бірдей «сан дөңгелегі» шыға бермейді. «Дөңгелек» шығу үшін әрдайым периодтағы цифр санының бөлшектің бөлімінен біреуі кем болуы керек.
Кейбір сандардан төмендегідей сатылар құрастыруға болады:

0*9+1=1,
1*9+2=11,
12*9+3=111,
123*9+4=1111,
1234*9+5=11111,
12345*9+6=111111,
12346*9+7=1111111,
1234567*9+8=11111111,
1234568*9+9=1111111111
9*9+7=88
98*9+6=888
987*9+5=8888
9876*9+4=88 888
98 765*9+3=888 888
987 654*9+2=8888 888
9876 543*9+1=88 888 888
98 765 432*9+0=888 888 888.
1*8+1=9
12*8+2=98
123*8+3=987
1234*8+4=9876
12 345*8+5=98 765
123 456*8+6=987 654
1234 567*8+7=9876 543
12 345 678*8+8=98 765 432
123 456 789*8+9=987 654 321.
Сандардың мұндай қасиеттерін арифметикалық жолмен, тікелей іздеп, табу өте қиын. Әдетте олар алгебралық өрнектер арқылы зерттеледі.
Кез келген екі таңбалы санды 50+r түрінде өрнектеуге болады. Онда R қосылғышы санының елуден қаншалықты артық немесе кем екендігін көрсетеді. Мәселен, 59 үшін r=9, ал 38 үшін r=-12 болады. Екімүшеліктің квадраты туралы теорема бойынша:
(50+r)2=2500+100r+r2.
Мұны былай жазуға болады:
(50+r)2=(25+r)*100+r2.
Бұдан мынадай ереже шығады: екі таңбалы санның квадратын табу үшін 25-ке берілген санның 50-ден артық бөлігін қосып (немесе 50-ге жетпей тұрған бөлігін шегеріп), 100 еселеу керек, содан соң оған әлгі бөліктің квадратын қосу керек. 25+r санын табу оңай. Жоғарыдығы мысалдар үшін 25+r=25+9=34 және 25+r=25 – 12 =13. Бұларды практикада 100-ге көбейтіп жатпайды, жүздіктердің орнына жазады. r2 мүшені ауызша есептеп қосады. Мысалы:
562=(25+6) 100+62=3100+36=3136,
432=(25 – 7 ) 100+72=1800+49=1849,
дәл осы тәсілмен:
632=3969, 742=5476,
382=1444, 422=1764.
Қорытынды
Осы ғылыми жобамды жазу барысында сандардың шаршыдағы негізгі қасиеттерінің қыр-сырымен таныстым. Жұмыс 1-ден 100-ге дейінгі натурал сандардың жүз торлы шаршыда орналасқаның зерттеу. Жүз торлы шаршылардың ішінен кез-келген өзі қалаған реттегі бір шаршыны таңдап алып, сол шаршыдағы сандардың қосындысын белгілі бір өрнек шығатындай есептегенде бір ғана қосындыға тең болатынын көрсете білдім. Сандардың шаршыдағы негізгі қасиеттерін зерттей отырып, негізгі теориясымен таныстым, оның қазіргі кездегі қолданысын зерттеген еңбегімде пәнге деген қызығушылығым артып, оқулықтарды пайдалана отырып ізденуімнің арқасында өзімнің біліміміді толықтырдым.
Қазіргі заман математика ғылымының өте кең, жан-жақты тараған кезеңі. Ал талапқа сай математикалық біліміді көтеру үшін оқушылардың әрқайсысының үлкен ізденісте жүруі шарт, яғни ғылыми жобамды басқа оқушылар керегіне қолданады деп ойлаймын. Қазіргі таңдағы қоғамның дамуының негізгі факторы – білім, ғылым және демографиялық, саяси тұрақтылық. Олай болса дәуір қанша құбылғанымен біздің жас болашағымыздың жақсы болуы білім ілімсіз жүзеге асуы мүмкін емес. Сондықтан да, еліміздің президенті Нұрсұлтан Әбішұлы Назарбаевтың білім мен ғылымның дамуына баса назар аударуы, оның үнемі өз бақылауында ұстауы соның айқын дәлелі.
Пайдаланылған әдебиеттер
1. Колмогоров А.Н. Современная математика и математика в современной школе // Математика в школе. – 1971. - №6. – С. 2-3.
2. Математика мен математиктер жайлы әңгімелер. М.Ө. Исқақов, С.Н. Назаров. Екінші кітап, «Мектеп» , 1970, 178 бет
3. Егемен Қазақстан, жалпыұлттық республикалық газет. №336 (25733), 2014 жыл,2б
4. Ғаламтор желісі bilimdiler.kz
Әлеуметтік желілерде бөлісіңіз:
Пікірлер (1)
Пікір қалдырыңыз
Қарап көріңіз
Басқа да жазбалар
- Мәдениет - Қазақ елінің рухани құндылықтарының қазынасы
- Тарихи тұлға - Ораз Жандосов
- «Жергілікті және оралған қазақтардың бірегейлік қақтығысы: қазақстандық көші-қон саясаты және репатрианттардың мәдени интеграциялануы мәселесі» жобасы
- Әл-Фараби мен түркі ғұламаларының мұрасындағы ізгі адам: компаративистік дискурс
- Өнер-білім бар жұртта…
- Сайып қыран саралаған "Жаңа кітап" Мұхамеджан Сералин
- Еліміздің жүз жыл бұрыңғы көрінісі
- Қазақстандағы ең төменгі табыстың көрсеткіші мен әлеуметтік аспектілері
- Желтоқсан — Тәуелсіздіктің бастауы
- Қазақстанға жер аударылған халықтар тарихы
- Қазақтың ұлттық бас киімдерінің семиотикасы
- Аккультурация мәдениетаралық коммуникацияның бір түрі ретінде
- Лидерлік дағдыларды түсіну және қолдау
- Бастауыш сыныптың “Көркем еңбек” сабақтарында оқушылардың шығармашылық іс-әрекетін дамыту мүмкіндіктері
- «Масс-медиа туралы» заң жобасын талдау



Бахтияр
Өте керемет жұмыс екен!!