Қошуш формулилири
Алматы облысы, Ұйғыр ауданы
"Долайты орта мектебі" КММ-сінің
математика және физика пәні мұғалімі
Даутова Махирям Телебалдыевна
9"ә" синип Алгебра
Дәрис мавзу си: Қошуш формулилири
Дәрис мәхсити: Қошуш формулилирини чүшәндүрүш; оқуғучиларниң есап чиқириш маһаритини ашуруш; оқуғучиларни уюшчанлиққа, коллективлиқ тәрбийләш
Дәрисниң типи: йеңи билимни өзләштүрүш
Дәрисниң усуни: чүшәндүрүш, соалға–жавап.
Пәнләр ара бағлиниши: тәбиәт, уйғур тили.
Көрнәклик қурал: таблица, карточкилар
Қолланған әдәбийәт: алгебра. 9-синип. А.Әбилқасымова, И.Бекбоев,А.Абдиева, З.Жумағулова
Дәрисниң бериши.
І. Уюштуруш.
ІІ. Өй тапшурмисини тәкшүрүш
§. №
ІІІ. Өткән материаллар бойича тәкрарлаш.
1. Еғизчә һесап
2. Карточка билән иш
ІV. Нәтижиләш.
Оқуғучиларниң жавави бойичә йәкүнләймән.
V. Йеңи материалға чүшүнүк.
Қошуш формулилири
Мәзкүр мавзуни оқуш жәриянида силәр немини үгинисиләр?
Мошу мавзуни өзләштүрүп, икки булуңниң қошиндиси вә айримисидики тригонометриялик функцияләрниң формулилирини билисиләр, мошу формулиларни тригонометриялик функцияләрни тәңму-тәң түрләндүрүш жәрuянuда қоллинишни үгинисиләр.
Мошу кәмгичә бир аргументқа бағлиқ тригонометриялик функцияләрниң арисидики нисбәтләрни беридиған формулиларни вә кәлтүрүш формулилирини қараштурдуқ. Улардин башқа тригонометриядә қошуш формулиси дәп атилидиған формулилар кәң қоллинилиду.
Ениқлима. Икки булуңнuң қошундиси вә айримисиниң тригонометриялик функциялирини шу булуңларнuң тригонометриялик финкциялири арқилиқ ипадиләйдиған формулиларни қошуш формилилири дәп атайду.
Алди билән тригонометриялик функцияләр арқилиқ икки булуңниң айриминиң косинусиниң формулисини чиқирайли. Униң үчүн, адәттикидәк, радиуси R=ОА болидиған, мәркизи тик булуңлуқ координата системисиниң башлинишида орунлашқан чәмбәрни қараштурайли (55-сүрәт).
ОА дәсләпки радиусини О чекитини айландуруп α вә β булуңлириға бураймиз. Нәтижидә, ОВ вә ОС радиуслириға мувапиқ келидиған ОА радиусиниң В вә С чекитлиридики орунлишиш hаләтлирини алимиз. Әгәр В чекитиниң координатилири х1 вә у1, әнди С чекитиниң координатилири х2 вә у2 болса, у чағда 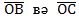 векторлириниң координатилири мувапиқ
векторлириниң координатилири мувапиқ 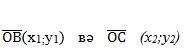 болидиғанлиғи геометрия курсидин бәлгүлүк.
болидиғанлиғи геометрия курсидин бәлгүлүк.
Әнди ОВ вә ОС векторлириниң скаляр көпәйтиндисини тапайли. Мошу икки векторниң скаляр көпөйтиндисини геометрия курсидин бәлгүлүк тәңлик билән йезишқа болиду:
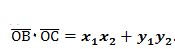 (1)
(1)
α вә β булуңлириниң синус вә косинусиниң ениқлимилири бойичә монуни елишқа болиду:
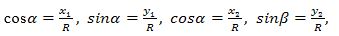
яки
x1= Rcosα, y1= Rsinα, x2= Rcosβ, y2= Rsinβ.
Мошу мәналарни (1) тәңликкә қойғанда келәси тәңлик чиқиду:
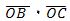 = R2cosαcosβ + R2sinαsinβ = R2 (cosαcosβ+sinαsinβ).
= R2cosαcosβ + R2sinαsinβ = R2 (cosαcosβ+sinαsinβ).
Шунда
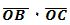 = R2 (cosαcosβ+sinαsinβ). (2)
= R2 (cosαcosβ+sinαsinβ). (2)
(2) формулиниң оң тәрәп бөлигигә икки векторниң скаляр көпәйтиндиси тоғрилиқ теоремини қоллинип, уни мундақ язимиз:
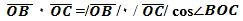 (3)
(3)
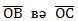 векторлириниң арисидики булуң ВОС булуңи яки α – β ға тәң булуң болуп hесаплиниду (56-сүрәт). Бирақ умумий түрдә ОВ вә ОС булуңлириниң арисидики ВОС булуңи α – β яки 2
векторлириниң арисидики булуң ВОС булуңи яки α – β ға тәң булуң болуп hесаплиниду (56-сүрәт). Бирақ умумий түрдә ОВ вә ОС булуңлириниң арисидики ВОС булуңи α – β яки 2 ға тәң яки толуқ булуңға һәссилик болидиған миқдарғила пәрқи болуши мүмкин (56-сүрәт).
ға тәң яки толуқ булуңға һәссилик болидиған миқдарғила пәрқи болуши мүмкин (56-сүрәт).
Шуниң үчүн барлиқ hаләтләрдә cos
Ахирқи тәңликни қоллинип вә / / = /
/ = / / = R векторлирини әскә елип, (3) тәңликтин:
/ = R векторлирини әскә елип, (3) тәңликтин:  ٠
٠  = R٠Rcos(α – β)
= R٠Rcos(α – β)
яки
 ٠
٠  = R2 cos(α – β) (4)
= R2 cos(α – β) (4)
алимиз.
(2) вә (4) тәңликлириниң сол тәрәп бөләклири тәң болғанлиқтин, уларниң оң тәрәп бөләклирини тәңләштүримиз, шунда
R2 cos(α – β) = R2 (cosα cosβ + sinαsinβ)
Буниңдин
cos(α – β) = cosα cosβ + sinαsinβ (5)
чиқиду. (5) формулини икки булуңниң айримисиниң косинуси дәп атайду.
Икки булуңниң айримисиниң косиниси мошу булуңларниң косинуслириниң көпәйтиндиси вә синуслириниң көпәйтиндисиниң кошундисиға тәң.
(5) формулини қоллинип, икки булуңниң кошундисиниң косинусини, йәни қошиндиниң косинусини оңай тепишқа болиду. Униң үчүн α + β қошундисини  айримиси түридә көрситәйли.
айримиси түридә көрситәйли.
cos(α+β) = cos чүнки cos(
чүнки cos( )=cosβ, sin(
)=cosβ, sin( β)=
β)= sinβ, йәни косинусниң жүплиги вә синусниң тағлиги әскә елинған.
sinβ, йәни косинусниң жүплиги вә синусниң тағлиги әскә елинған.
Шундақ қилип, қошиндиниң косинуси дәп атилидиған формулини алдуқ:
cos(α + β) = cosα cosβ  sinαsinβ (6)
sinαsinβ (6)
Икки булуңниң қошиндисиниң косинуси мошу булуңларниң косинуслириниң көпәйтиндисигә вә синуслириниң көпәйтиндисиниң айримисиға тәң.
Әнди икки булуңниң қошундиси вә айримисиниң синусиниң формулисини чиқирайли. Униң үчүн (5) тәңликни вә кәлтүрүш формулисини қоллинайли. Шунда
sin(α+β) = cos , кәлтүрүш формулиси бойичә
, кәлтүрүш формулиси бойичә
 .
.
Шуниң үчүн
sin(α + β) = sin α cosβ + cos α sin β (7)
Икки булуңниң айримисиниң синуси биринчи булуңниң синусиниң иккинчи булуңниң косинусиға көпәйтиндиси вә биринчи булуңниң косинусиниң иккинчи булуңниң синусиға көпәйтиндисиниң қошундисиға тәң.
(7) формулини қоллинип, икки булуңниң айримисиниң синусиниң формулисини оңай йол билән тепишқа болиду.
Шуниң билән,
sin(α – β) = sin
чүнки 
Шуниңдин
 =
= (8)
(8)
Икки булуңниң айримисиниң синуси биринчи булуңниң синусиниң иккинчи булуңниң косинусиға көпәйтиндиси вә биринчи булуңниң косинусиниң иккинчи булуңниң синусиға көпәйтиндисиниң айримисиға тәң.
Әнди (5)-(8) вә синус билән косинус арқилиқ ипадилинидиған формулилирини қоллинип, тангенс вә котангенс үчүн қошуш формулилирини чиқириш қийин әмәс.
Мисал үчүн қошундиниң тангенсиниң формулисини хуласиләп чиқирайли:
tg(α + β) =  . Әнди cosα
. Әнди cosα вә cosβ
вә cosβ дәп елип, ахирқи кәсирниң сүрити билән мәхрижини cosα ٠ cosβға бөләйли. Шунда
дәп елип, ахирқи кәсирниң сүрити билән мәхрижини cosα ٠ cosβға бөләйли. Шунда

Демәк,
tg(α + β) = (9)
(9)
Дәл мошундақ икки булуңниң айримисиниң тангенсиниң формулисини
мустәқил испатлаңлар.
tg(α  β) =
β) = (10)
(10)
(9) вә (10) формулиларни бириктүрүп, умумий турдә мунлақ йезишқа болиду:
 (11)
(11)
Икки усули билән қошундиниң тангенси вә котангенсиниң формулилириниң һәқиқийлигини мустәқил испатлаңлар.
 (12)
(12)
1-мисал. Жәдвәлни пайдиланмай вә микрокалькуляторниң ярдимисиз cos 105º-ниң мәнасини тепиңлар.
Йешиш. Униң үчүн 105º-ни 60º + 45º қошундиси түридә язимиз. Шунда
cos105º =cos(60º + 45º)=cos60ºcos45º - sin60ºsin45º=
2-мисал. cos(α+β) – cos(α – β) ипадисини ихчамлайли.
Йешиш. Униң (5) вә (6) формулиларни қоллиниду. Шунда cos(α+β) – cos(α – β)=cosαβ – sinαsinβ – cosαcosβ – sinαsinβ = – 2sinαsinβ
3-мисал. Әгәр tgα =  вә β тар булуңлар болса, у чағда α + β булуңлириниң қошундисини тапайли.
вә β тар булуңлар болса, у чағда α + β булуңлириниң қошундисини тапайли.
α + β қошундисини тепиш үчүн (9) қошундиниң тангенси формулисини қоллинимиз, у чағда
tg(α + β) =  .
.
tg(α + β) = 1 буниңдин α + β = 45ºқа тәң. Жавави:45º.
VI. Һесап чиқириш. №
VІІ. Нәтижиләш. Оқуғучилар чиқарған һесаплири бойичә йәкунләймән.
VІІІ. Өйгә тапшурма. §
Пікірлер (1)
Пікір қалдырыңыз
Қарап көріңіз
Басқа да жазбалар
- 9 санының құрамы
- Қазақ музыка өнерінің гималайы-Ахмет Жұбанов.
- «Алтыбақан аясында» атты Үкілі Ыбырай Сандыбайұлының өмірі мен шығармашылығына арналған театрландырылған қойылым
- Технология - 5 сынып
- Қыс
- Құстар – біздің досымыз!
- Ақылды тыңдай білу де өнеге
- Ит – жеті қазынаның бірі
- Балқаш көліне саяхат
- Біз толеранттымыз...
- Технология 11, сынып аптасына -1 сағат, оқу жылына -34 сағат
- Ғажайып бақ ертегісі
- Жер және су
- Күз – мереке, күз – береке
- «Ғажайып алаң » интеллектуалдық ойыны.



- Илон Маск
- Фирдауси
- Әл-Жахиз
- Марк Аврелий
Барлық авторлар
Ілмек бойынша іздеу
Мақал-мәтелдер
Қазақша есімдердің тізімі