Сызықты программалау есептерін Симплекс әдісімен шешу

«Түркістан гуманитарлық-техникалық колледжі» МКҚК
арнайы пәндер оқытушысы
Абилхаирова Меруерт Абилхаирқызы

 

СП есептерінің шешімін табу үшін бірнеше әдістер қолданылады. Олардың ішінде кең тараған графиктік әдіс және симплекс әдісі.

Графиктік әдіс есептің геометриялық мәнінде негізделген және көбінесе екіөлшемді жазықтық есептерін шешуде қолданылады.

Симплекс әдісі – сызықты программалау есептерінің барлық өлшемді түрлерін есептеуге пайдаланатын әдіс. Егер де СП есебіне айнымалылар саны өтек өп болса, бұл жағдайда компьютерлік программалар арқылы есептің тиімді шешімін табады. Мысалы, Excel көмегімен.

Симплекс әдісі сызықты программалау есептерінің шешімін табу үшін әмбебап әдіс.

Симплекс әдісінің алгоритмі

1. Есепті негізгі түрге келтіру.

2. Шектеулер жүйесінің теріс емес базисті шешімін анықтау.

3. Бос айнымалылардың бағаларын есептеу ∆_j=∑c_ih_ij-c_j, j=1,n, мұнда h_ij – бос айнымалылардың алдындағы коэффициенттер х_j, c_i- мақсатты функциядағы базисты айнымалылардың коэффициенттері, c_j – мақсатты функциядағы бо айнымалының коэффициенті.

4. Табылған тірек шешімді тиімділік шартына тексеру:

А) егре барлық бағалар ∆_j≥0, онда табылған шешім тиімді және есептің шешімі табылды деп айтуға болады

Б) егер де бір ғана баға ∆_j<0, ал сәйкесінше айнымалының коэффициенттерінің ішінде оң сан болмаса, онда есептің тиімді шешімі жоқ  деп айтуға болады

В) егер де бір ғана баға ∆_j<0, ал сәйкесінше айнымалының коэффициенттерінің ішінде бір ғана оң сан болса, онда табылған шешім тиімді емес, және басқа базисты таңдап, оны жақсартуға болады. Егер де теріс бағалар бірнеше болса, онда базис ретінде бағалардың абсолютті мәні ең жоғары көрсеткіш арқылы айнымалыны таңдаймыз.  

1. Ескерту. СПЕ минимумға ұмтылатын жағдайда тиімділік критериі ретінде бағалардың терістігі саналады.

2. Ескерту. СПЕ мақсатты функция максимумы және минимумы  жалпы болып саналады.

Есеп 1.

Берілген СП есебін симплекс әдісімен шешу.

F=2,4X₁+1,6X₂→max

0,8X₁+1,6X₂+X₃=4,8

1,6X₁+0,8X₂+X₄=6,4

X₂+X₅=2

X₁,X₂,X₃,X₄,X₅≥0

Шешімі:

Теңдіктер жүйесін векторлық түрде жазамыз.

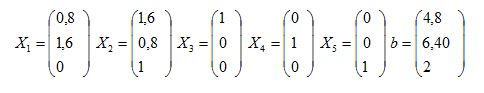
i=1,3

Х1,Х2,Х3,Х4,Х5 векторлар арасында 3 бірлік векторлар болғандықтан, есептің бастапқы тірек жоспарын жазуға болады.

Хт=(0;0;4,8;6,4;2)

Бастапқы тірек жоспарын тиімділік шарытан тексереміз, ол үшін бірінші симплекс кестені құрастырамыз:

1 кесте

Базис	Сб	В	Х1↓	Х2	Х3	Х4	Х5	Q
			2,4	1,6	0	0	0
Х3	0	4,8	0,8	1,6	1	0	0	6
←Х4	0	6,4	1,6	0,8	0	1	0	4
Х5	0	2	0	1	0	0	1	-
∆j		0	-2,4	-1,6	0	0	0

 

1 итерация үшін: Z1-C1=-2.4, Z2-C2=-1.6 бағалар теріс болып тұр. Кестедегі Х₁,Х₂ айнымалылардың мәндері 0-ге тең, сондықтан бұл жоспар тиімді емес.

Екінші симплекс кестеге көшу үшін бағыттаушы бағана мен бағыттаушы жолды анықтаймыз: 2,4>1,6, яғни бағыттаушы бағана – Х₁ бағанасы.

Бағыттаушы жолды анықтау үшін, Q бағанасында келесіні есептейміз:

Q=min(B/aij), aij>0, яғни есептеуіш элемент – 1,6.

Екінші симплекс кестесін толтырған жағдайда келесіні ескертеміз: Х₄ айнымалысы базистан шығады, ал Х₁ айнымалысы базиска кіреді.

2 кесте

Базис	Сб	В	Х1	Х2↓	Х3	Х4	Х5	Q
			2,4	1,6	0	0	0
←Х3	0	1,6	0	1,2	1	-0,5	0	1,3
Х1	2,4	4	1	0,5	0	0,6	0	8
Х5	0	2	0	1	0	0	1	2
∆j		9,6	0	-0,4	0	1,5	0

Екінші симплекс кестені толтыру ережесі:

1. Екінші симплекс кестесінде екінші жолда Х₄ айнымалысының орнына Х₁ айнымалысын жазамыз

2. Бірінші симплекс кетесінің екінші жолдын барлық элементтерін 1,6 есептеуіш элементіне бөлеміз

3. 2 Симплекс кестесінің қалған элементтерін үшбұрыш ережесімен толтырамыз: мысалы В бағанасының және Х3 жолының қиылысында орналасқан санды келесідей анықтаймыз:4,8-0,8*4=1,6. Кестенің қалған элементтері сәйкесінше толтырылады.

2 итерация үшін: Z2-C2=-0,4 бағасы теріс болып тұр, сондықтан бұл жоспар тиімді емес.

Үшінші симплекс кестеге көшу үшін бағыттаушы бағана мен бағыттаушы жолды анықтаймыз: бағыттаушы бағана – Х₂ бағанасы.

Бағыттаушы жолды анықтау үшін, Q бағанасында келесіні есептейміз:

Q=min(B/aij), aij>0, яғни есептеуіш элемент – 1,2.

Үшінші симплекс кестесін толтырған жағдайда келесіні ескертеміз: Х₃ айнымалысы базистан шығады, ал Х₂ айнымалысы базиска кіреді.

3 кесте

Базис	Сб	В	Х1	Х2↓	Х3	Х4	Х5	Q
			2,4	1,6	0	0	0
Х2	1,6	1,33	0	1	0,8	-0,4	0
Х1	2,4	3,33	1	0	-0,4	0,8	0
Х5	0	0,66	0	0	-0,8	0,4	1
∆j		10,1	0	0	0,3	1,3	0

Үшінші симплекс кестесіне қарайтын болсақ, барлық бағалар оң сандар, яғни бұл шешім тиімді болып табылады:

Хт=(3,33; 1,33; 0; 0; 0,66), ал мақсатты функция мәні F=10,1 тең.

---