Математикалық индукция методы және оның қолданылуы

Мырзақұлова Назерке Базарәліқызы

Қазақ Ұлттық Қыздар Педагогикалық Университеті

Алматы қ., Қазақстан

Аңдатпа. Математикалық индукция әдісін жан-жақты және терең зерттеу, оның пайда болған кезінен бастап математиканың қазіргі даму деңгейіне дейін қолданылуы. Математикалық индукция әдісін математикалық есептердің әртүрлі түрлерін шешуге қолдану.

Түйін сөздер: Индукция, әдіс, математика.

Математикаға тән белгілердің бірі дедуктивті теорияны құру болып табылады, бірақ дедукция ғылыми ойлаудың жалғыз әдісі емес. Эксперименттік ғылымдарда индуктивті қорытындылардың рөлі зор. Мысалы, математикада индукция көбінесе теоремаларды тұжырымдауға көмектеседі, ал кейбір басқа жағдайларда тіпті дәлелдеу жолын белгілеуге көмектеседі.

Бұл тақырып бүгінде өзекті болып табылады, математикалық индукция әдісінің қолдану аясы кеңейді. Бірақ, өкінішке орай, мектеп бағдарламасы бұл тақырыпты зерттеуге аз уақыт бөледі. Материалды талдау үшін көбінесе бірнеше сабақ бөлінеді, оның барысында теория беріледі және бірнеше қарапайым есептер талданады. Математиканы тереңдетіп оқытпайтын мектептерде бұл әдіс оқу бағдарламасына мүлде енбеген. Дегенмен, еліміздің жетекші жоғары оқу орындарына түсу емтихандарында математикалық индукция әдісін шешуді қажет ететін есептер бар.

Кез келген математикалық зерттеулердің негізі дедуктивті және индуктивті әдістер болып табылады. Қорытындылаудың дедуктивті әдісі жалпыдан жекеге қарай пайымдау, яғни бастау нүктесі жалпы нәтиже, ал соңғы нүктесі жеке нәтиже болып табылатын пайымдау. Индукция жеке нәтижелерден жалпыға өтуде қолданылады, яғни ол дедуктивтікке қарама-қарсы әдіс. Эксперименттік ғылымдарда индуктивті қорытындылардың рөлі өте зор. Олар шегерім арқылы одан әрі қорытындылар жасалатын ережелерді береді.

Математикалық индукция принципі, дәл екі қадамның таныс түрінде, алғаш рет 1654 жылы Блез Паскальдің «Арифметикалық үшбұрыш туралы трактат» еңбегінде пайда болды, онда комбинациялар санын (биномдық коэффициенттер) есептеудің қарапайым тәсілі индукция арқылы дәлелденді. .

Математикалық индукция әдісі математикалық индукция принципіне негізделген, ол келесідей:

1. Бұл мәлімдеменің дұрыстығы n = 1  үшін тексеріледі (индукциялық негіз),

2. бұл тұжырымның дұрыстығы  n = k  үшін қабылданады, мұндағы k - ерікті натурал сан (индукциялық жорамал) және осы болжамды ескере отырып, оның дұрыстығы n = k + 1 (индукция қадамы немесе индукциялық ауысу) үшін белгіленеді.

Белгілі бір тұжырымды  n - ге байланысты толық емес математикалық индукция арқылы дәлелдеу, мұндағы n², ұқсас жолмен жүзеге асырылады, бірақ алдымен n - нің ең кіші мәнінің дұрыстығы белгіленеді.

Математикалық индукция әдісі - математикалық индукция принципін қолдануға негізделген гипотезаны (мәліметтерді) дәлелдеудің тиімді әдісі болып табылады, сондықтан ол тек дұрыс қорытындыға әкеледі. Математикалық индукция әдісі барлық есептерді шеше алмайды, тек индукциялық айнымалы деп аталатын белгілі бір айнымалымен параметрленген есептерді шеше алады. Математикалық индукция әдісі арифметикада, алгебрада және сандар теориясында кеңінен қолданылады. Математикалық индукция әдісі математикалық есептердің көптеген түрлерін шешудің әмбебап құралы болып табылады.

Математикалық индукция әдісін қолданудың негізгі саласы әртүрлі сәйкестіктерді дәлелдеу болып табылады. Осы типтегі есептерді шешудің бірнеше мысалдарын қарастырайық.

1-мысал. Кез-келген нақты a  саны мен кез-келген  m және n  натурал сандары үшін aⁿ∙a^m=a^(n+m)  теңдігі дұрыс болатынын дәлелдеңдер.

Дәлелдеу:  m  ерікті натурал санын көрсетейік және олар айтқандай,  n  бойынша индукцияны қолданайық.

1. n = 1  үшін теңдік натурал көрсеткішті дәреженің анықтамасы арқылы ақиқат болады:.

a¹∙a^m=a^(1+m)

2. Енді n = k  үшін теңдігіміз ақиқат болсын:

a^k∙a^m=a^(k+m)

3. Оның n = k + 1 үшін де дұрыс екенін дәлелдейік:

a^m∙a^(k+1)=a^(m+k+1)

Содан кейін, индукциялық гипотеза және дәреженің анықтамасы бойынша бізде:

a^m∙a^(k+1)=a^m∙a^k∙a¹=a^(m+k)∙a¹=a^(m+k+1),
яғни a^m∙a^(k+1)=a^(m+k+1)

Демек, математикалық индукция принципі бойынша теңдік ерікті түрде таңдалған m үшін кез келген натурал n саны үшін ақиқат болады, яғни кез -келген m  және n  натурал саны үшін ақиқат.

2-мысал. Кез-келген  n > 1 натурал саны үшін теңдік ақиқат болатынын дәлелдеңдер.

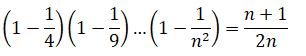
Дәлелдеу: Бұл сәйкестікті барлық  n > 1 үшін дәлелдеу керек екенін ескеріңіз, яғни, индукциялық базис n - нің келесі табиғи мәні үшін, яғни  n = 2 үшін тексеріледі.

1. n = 2  үшін  аламыз дұрыс, сондықтан математикалық индукция принципінің бірінші шарты орындалады.

2. n = k  үшін формула дұрыс деп есептейік: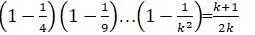 

3. n = k + 1 үшін оның дұрыстығын дәлелдейік: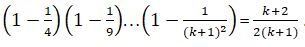

Бірінші  k   көбейткіштерді 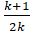  (2-қадам болжамы бойынша) ауыстырып, кейбір түрлендірулерді орындаймыз:

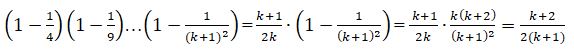
Сонымен, математикалық индукция принципінің екінші шарты да орындалады. Формула дәлелденді.

Математикалық индукция әдісі кейбір тригонометриялық есептерді шешуге де қолданылады. Осы мысалды қарастырайық.

3-мысал. 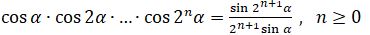  теңдігін дәлелдеңдер.

Дәлелдеу: сәйкестікті математикалық индукция арқылы дәлелдейік.

1. n = 0 үшін 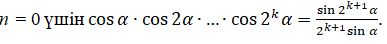 аламыз.

2. n = k + 1  үшін сәйкестік ақиқат болсын:     

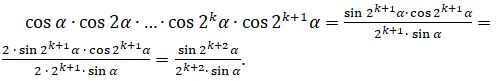
Демек, теңдік ақиқат (математикалық индукция әдісі бойынша).

Математикалық индукция әдісін қатарларды қосуға қолдану. Қатарлардың қосындысы сәйкестіктердің ерекше түрі болып табылады. Көптеген белгілі формулалар математикалық индукция әдісімен дәлелденген, олардың бірі арифметикалық прогрессияның алғашқы n мүшесінің қосындысының формуласы.

4-мысал. Арифметикалық прогрессияның алғашқы  n мүшесінің қосындысының формуласын дәлелдеңдер.

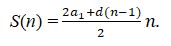
Дәлелдеу:

1. n = 1  үшін 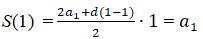 (ақиқат, өйткені арифметикалық прогрессияның бірінші мүшесінің қосындысы тең осы прогрессияның бірінші мүшесі).

2. n = k  үшін формула ақиқат болсын делік: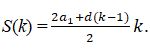 

3. n = k + 1  формуласының дұрыстығын дәлелдеп көрейік:

 

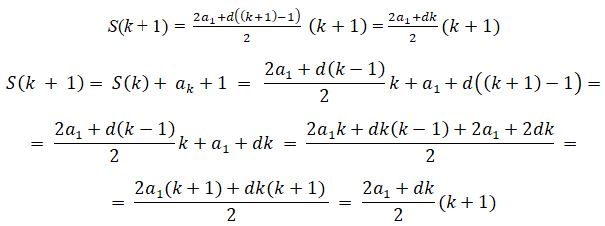
Математикалық индукция әдісі арқылы формула дәлелденеді.

Теңсіздіктерді дәлелдеуге математикалық индукция әдісін қолдану. Математикалық индукция әдісін қолдана отырып, көптеген теңсіздіктерді дәлелдеуге болады. Бұл әдіс осы салада кең таралмағанымен, индукция арқылы теңсіздіктерді дәлелдеу қиын болуы мүмкін, бірақ ол әлі де пайдалы болуы мүмкін.

5-мысал. 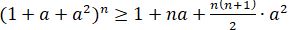теңсіздігі  a > 0 үшін барлық  n натурал сандар үшін дұрыс екенін дәлелдеңдер.

Дәлелдеу:

1. n = 1  үшін екі жағы тең: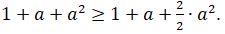

2. n = k  үшін 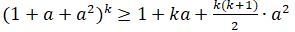 теңсіздігі орындалсын делік.

3. Теңсіздік n = k + 1  үшін де ақиқат болатынын дәлелдеп көрейік  

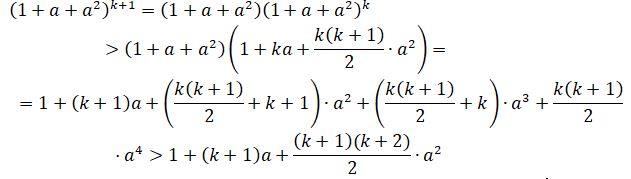
Сонымен, n = k + 1  үшін теңсіздік ақиқат, сондықтан математикалық индукция әдісі бойынша тұжырым кез-келген натурал n саны үшін ақиқат болады.

Математикалық индукция әдісін қолданып шығарылатын есептер контексінде дәлелдеуді қажет ететін жалпы заңдылық әрқашан нақты тұжырымдала бермейді. Кейде жекелеген жағдайларды бақылай отырып, алдымен олардың қандай жалпы заңдылыққа әкелетінін анықтау (болжау), содан кейін ғана математикалық индукция әдісімен айтылған гипотезаны дәлелдеу қажет. Сонымен қатар, индукциялық айнымалыны бүркемелеуге болады және мәселені шешу алдында индукция қандай параметр бойынша жүзеге асырылатынын анықтау керек.

Қорытынды. Математикалық индукция әдісі - математикалық есептердің алуан түрін шешудің теориялық негіздерінің бірі болып табылады. Бұл әдісті есептеулерде, сәйкестіктерді, теңсіздіктерді дәлелдеуде, тригонометриялық және арифметикалық есептерді шешуде, элементар математикада теоремаларды дәлелдеуде қолданылады.

Математикалық индукция әдісі белгілі бір бақылауларға сүйене отырып, сәйкес жалпы заңдылықтар туралы қорытынды жасауға мүмкіндік беретін және бұл әдісті нақты мысалдар арқылы түсінуге оңай болатын математикалық дәлелдеудің ерекше әдісі болғандықтан, мен өз жұмысымда осыған байланысты көптеген мәселелерді қарастырдым

ӘДЕБИЕТТЕР  ТІЗІМІ

1. Боковнев О.А., Фирсов В.В., Шварцбурд С.И. Математиканың таңдамалы сұрақтары. 9 сынып. Факультативтік курс.- М.: Білім, 1979.

2. Виленкин Н.Я.Индукция. Комбинаторика. Мұғалімдерге арналған нұсқаулық. М.: Білім, 1976 ж.

3. Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. Математика оқулығының беттері. Мәскеу: Білім, 1996 ж.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И.Алгебра және математикалық талдау курсын тереңдетіп оқыту: әдістемелік ұсыныстар, дидактикалық материалдар.

5. Иванова Е.Ю.Олимпиада мәселелері: ММФФ сырттай бөлімінің студенттеріне арналған әдістемелік әзірлеме – М.: ММУ механика-математика факультетінің қолданбалы зерттеулер орталығының баспасы, 2008 ж.

6. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х. Пайдасы

жоғары оқу орнына түсушілерге арналған математика. - М., Наука, 1981 ж.

7. Соминский И.С. Математикалық индукция әдісі. Математикадан танымал лекциялар, 3 шығарылым – М.: Наука, 1974.

8. Петраков И.С. 8-10 сыныптардағы математикалық үйірмелер: Кітап. Мұғалім үшін М.: Білім, 1987 ж.

---

Әлеуметтік желілерде бөлісіңіз: