Иррационал теңдеулер мен теңсіздіктерді шешудің жолдары

Шығыс Қазақстан облысы Семей қаласы
Семей қаласының Шәкәрім атындағы мемлекеттік университетінің
«5В010900» - математика мамандығының студенттері
Нурланова Эльнара, Абдисаматова Гулдана   
Ғылыми жетекшісі – Қ. Р. Тайболдина

Аннотация

Мақала мектеп математика курсында иррационал теңдеулер мен теңсіздіктерді оқытудың ерекшеліктеріне арналған. Арнайы есептер шығару жолдары көмегімен осы тақырыпты  оқытудың ерекшеліктерімен және кезеңдерімен танысуға ерекше көңіл бөлінеді.

Кілт сөздер: мектептегі иррационал теңдеулер мен теңсіздіктер, теңдеулер мен теңсіздіктер жүйесі, анықталу облысы.

Теңдеулер ұғымымен оқушылар төменгі сыныптардан таныс. Бүтін коэффцентті алгебралық, бөлшек рационал, қарапайым тригонометриялық және иррационал теңдеулер мен теңсіздіктерді шешу көп қиындық тудырмайды. Ал теңдеулер түбірлерінің рационал не иррационал болатындығын, олардың коэффициценттеріне байланысты теңдеудің түбірлері бар не жоғын анықтау, теңдеу шешімін табу үшін оның анықталу облысын ескере отырып түрлендіру оқушылар үшін біршама қиындықтар тудыратындығы белгілі.

Теңдеулер мен теңсіздіктердің шешімін іздестіруде өрнектің анықталу облысының маңызы зор. "Анықталу облысы" түсінігі "функция" ұғыммен тығыз байланысгы.

Теңдеулер мен теңсіздіктерді шешу барысында функцияның берілу жиыны мен олардың қиылысуы, әртүрлі түрлеңдірулер т.с.с. басқа да мағлұматтар мен түсініктер қамтылады және олардын барлығы логикалық талдаулар тұрғысында жүзеге асырылады.

Егер берілген теңдеудің әрбір шешімі екінші бір теңдеудің де шешімі болса онда екінші теңдеу берілген теңдеудің салдары деп аталды.

Егер екі теңдеудің бірінің шешімі екіншісінің де шешімі болса онда ол теңдеулер мәндес(эквивалентті) деп аталады.

Берілген теңдеуден онын салдары болатын теңдеу алу үшін келесі амалдарды орындауға болады:

1) теңдеудің екі жағына, оның анықталу облысында анықталған функцияны қосуға немесе шегеруге және көбейтуге;

2) теңдеудің екі жағын, оның анықталу облысында анықталған нөлге тең емес функцияда бөлуге;

3) егер g₁(x)*g₂(x)*...*g_n(x)=0 түріндегі теңдеу берілсе, онда келесі теңдеулер жиынтығы, оның салдары болады:

g₁(x)=0, g₂(x)=0, ... , g_n(x)=0

Тендеулерді түрлендіру кезінде оның анықталу облысы өзгеруі мүмкін. Сондықтан табылған шешімдерді берілген теңдеуге қойып тексеру керек.

Берілген теңдеуден онымен мәндес (эквивалентті) теңдеуге көшу үшін келесі амалдарды орындауға болады:

1) теңдеудің екі жағына, оның анықталу облысында анықталған функцияны қосуға немесе екі жағынан шегеруге;

2) теңдеудің екі жағын да, оның анықталу облысында анықталған нөлге тең емес функцияға көбейтуге не бөлуге;

3) теңдеудің екі жағын так дәрежеге шығаруға;

4) егер теңдеудің екі жағындағы функциялардың мәндері теріс емес болса, онда екі жағын жұп дәрежеге шығаруға.

Иррационал теңдеулерге қатысты келесідей кестені ұсынуға болады.

Иррационал теңдеулерді шешу барысында келесі амалдарды жасауға болмайды:

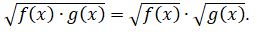Бұл амал теңдеудің анықталу облысын тарылтады.

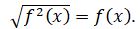Бұл теңдік тек қана 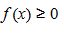болғанда орынды. Жалпы жағдайда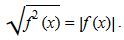

Енді аталған тақырыпқа қатысы бірнеше есептерді қарастырайық.

l. 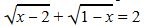 теңдеуін шешіңіз.

Шешуі. Бұл теңдеуді екі жағын да квадраттау немесе теңдеулер жүйесіне келтіру әдістерімен шешуге болады. Осы әдістердің әрқайсысы да біршама есептеулер жүргізуді қажет етеді. Күрделі есептеулерсіз теңдеудің шешімін анықтауға мүмкіндік беретін әдісті қарастырайык. Осы мақсатта, функцияның анықталу облысын табамыз. Ол келесі теңсіздіктер жүйесінің шешімі:

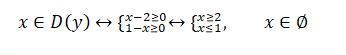
Яғни,  теңдеудің шешімі жоқ.

Кейде анықталу облысы ақырлы нүктелер жиынынан тұрады, ондай жағдайда теңдеудің шешімі больш табылатындарын олардың арасынан тексеріп, таңдау ғана жеткілікті. Ал кей жағдайларда анықталу облысы ақырлы нүктелер жиынынан тұрмайды, сондыктан біp қарағанда, теңдеу анықталу облысын зерттеу жолымен шешілмейтін болып көрінеді. Бірақ анықталу облысын табу тәсілін теңдеуді шешудің әр қадамында қолдануға болады.

2. 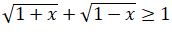 теңсіздігін шешіңіз.

Шешуі. 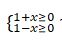  теңсіздіктер жүйесінің шешімі  -1≤ х≤ 1 екендігін көру қиын емес. Яғни, берілген өрнектің анықталу облысы  -1≤ х≤ 1

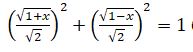болғандықтан, 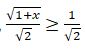немесе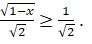

Сондықтан, 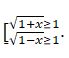. Онда  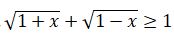теңсіздігі анықталу облысына тиісті барлық  x үшін орындалады. Демек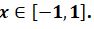

3. 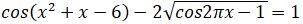 тендеуін жүйесін шешіңіз.

Шешуі. Теңдеудің тікелей анықтау мүмкін еместіктен, анықталу облысын табайық. Ол үшін cos2πх-1≥ 0 , яғни cos2πх≥ 1 теңсіздігінің шешімдерін анықтау керек. Соңғы теңсіздіктен cos2πх=1 болатындығы айқын. Сонымен, анықталу облысы х=k, k∈Z . Табылған мәндерді берілген теңдеуге қойып, оны қанағаттандыратындарын анықтайық. Сонда cos(k²+k-6) =1 теңдеуін аламыз. Осыдан (k²+k-6) = 2πn, мұндағы . n, k∈Z Соңғы теңдеудің сол жағындағы өрнек бүтін сан, ал оң жағындағысы бүтін емес екендігін көреміз. Сондықтан теңдік тек қана n = 0 болғанда орындалуы мүмкін.

Енді (k²+k-6) = 0 теңдеуін шешеміз. Оның түбірлері k = 2 және k = -3 . Демек, тендеудің шешіндері x = 2 және x = -3 .

Біз бұған дейін теңдеулер мен теңсіздіктерді шешуде анықгалу облысына көңіл бөлдік. Бірақ осы әдісті қолдануға келмейтін тапсырмалар да кездеседі. Кей жағдайда иррационал тендеулер мен теңсіздіктердің шешімін анықтау үшін, түйіндесіне көбейту әдісін қолдануға болады

4. теңдеуін шешіңіз.

Шешуі.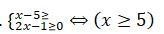

Теңсіздіктер жүйесі деп қарастырсақ, қате жіберген болар едік. Себебі теңдеудің оң жақ бөлігі ескерілмей отыр. Ол нольден үлкен, сондықтан теңдеудің анықталу облысы келесі теңсіздіктер жүйесінің шешімі болады:

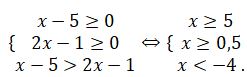
Демек, теңдеудің шешімі жоқ.

5. 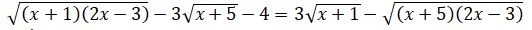 теңдеуін шешеміз.

Шешуі. Теңдеудің екі жағын квадраттасақ берілген теңдеуден де күрделі теңдеу аламыз. Сондықтан, берілген теңдеуді келесідей түрлендірейік: Теңдеудің coл жағындағы өрнекті көбейткіштерге жіктесек  теңдеуіне келеміз. Әдетте, тендеудің оң жағында 0 болғанда көбейткіштерге жіктейді. Берілген теңдеу жағдайында коэффиценттерге байланысты, теңдеудің шешімі жеңіл табылады. Соңғы теңдеудің екі жағын да бірінші жақшадағы өрнектің түйіндесіне көбейтейік, яғни,  өрнегіне. Онда  

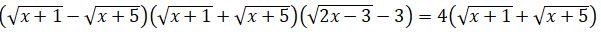Осыдан  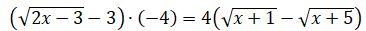немесе  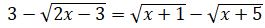болады. Соңғы теңдеудің екі жағын да квадраттасақ  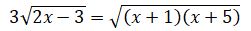теңдеуіне келеміз. Басқаша топтастырып квадраттау, берілген теңдеуден де күрделі теңдеуге әкеледі. Соңғы теңдеудің екі жағын да квадраттап,

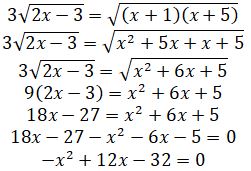
x² -12x +32 = 0 теңдеуін аламыз. Осыдан, x = 8 және x = 4. Табылған шешімдерді теңдеуге қойып тексеріп, оның шешімі x = 8 екендігін көреміз.

Иррационал теңдеулер мен теңсіздіктерді шешудің жолдарын талдауда мектеп математикасының негізгі теориялық материалы қамтылады. Тақырыпты дұрыс меңгеру үшін теңдеулер классификацияланып, олардың әрқайсысы бойынша оны шешудің әдіс-тәсілдері таңдалып, меңгерілу деңгейі тексерілетіндігі белгілі. Мұқият іріктеліп, мүмкіндігінше толық баяндалған теориялық материал, есеп қойылымын және оны шешудің тәсілдерін үйренуді қамтамасыз етумен қатар, қатаң логикалық талдауларды меңгеруде де септігі тиер деген ойдамыз.

Пайдаланған әдебиеттер:

1. «Самұрық» математикалық зияткерлік сайысына берілген есептерді шығаруға арналған әдістемелік құрал (5-7 сынып)
2. А. И Прилепко «Сборник задач по матиматике» Москва, 1983
3. З. К Айназарова «Справочник школьника по математике», «Арман-ПВ», 2007ж

---

Әлеуметтік желілерде бөлісіңіз: