Фибоначчи сандары: іш пыстырмайтын математикалық фактілер

Баршамызға математиканың барлық ғылымдардың ішіндегі ең басты ғылым екені белгілі. Алайда, көптеген адам бұнымен келіспеуі мүмкін, өйткені кейде математика — тек есептер мен мысалдар және сол сияқты адамды зеріктіретін нәрселердей көрінеді. Дегенмен, математика бізге таныс заттарды мүлдем бейтаныс жағынан оп-оңай көрсетіп бере алады. Оның үстіне — ол тіпті әлемнің құпияларын ашып бере алады. Қалайша дейсіз бе? Фибоначчи сандарына жүгініп көрейік.    

Фибоначчи сандары дегеніміз не?  

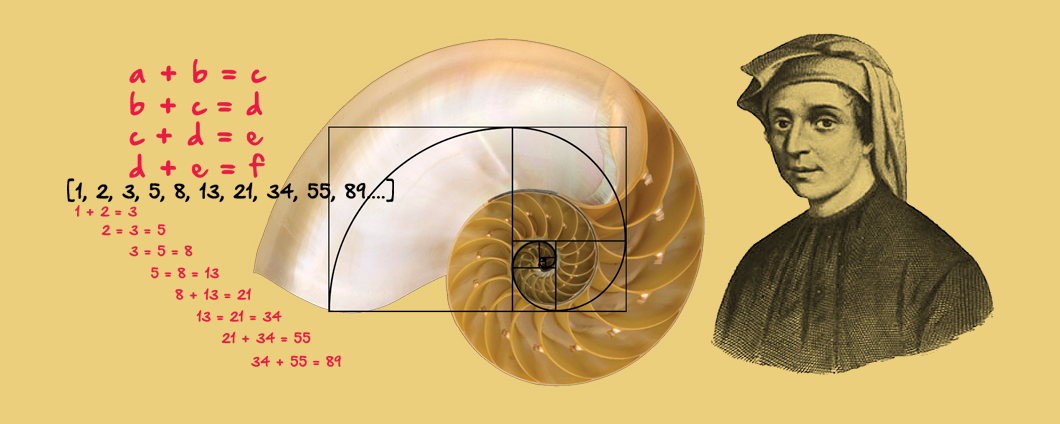
Фибоначчи сандары деп келесісі алдындағы екі санның қосындысынан шығатын сандар тізбегі аталады, мысалы, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Әдетте бұндай тізбек F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2, n ≥ 2 формуласы арқылы жазылады.  

Фибоначчи сандары теріс «n» мәнінен басталуы мүмкін, бірақ бұндай жағдайда тізбек екіжақты болады — ол екі бағытта да шексіздікке қарай ұмтылатын оң және теріс сандарды қамтиды. Бұндай сандар тізбегінің мысалы мынау бола алады: -34, -21, -13, -8, -5, -3, -2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ал оның формуласы мынандай болмақ: F_n = F_n+1 — F_n+2 немесе F_-n = (-1)ⁿ⁺¹F_n.  

Фибоначчи сандарын құрушы Орта ғасырлық Европаның алғашқы математиктерінің бірі Пизалық Леонардо еді. Оны көпшілік Фибоначчи деген атынан таниды — бұл лақап атты ол қайтыс болған соң көп жыл өткенде барып алды.  

Көзі тірісінде Пизалық Леонардо математикалық турнирлерді қатты жақсы көрді, осы себепті ол өз еңбектерінде («Liber abaci» /«Абак кітабы», 1202; «Practica geometriae»/«Геометрия практикасы», 1220, «Flos»/«Гүл», 1225 жыл — кубтық теңдеулер тақырыбына арналған зерттеу және «Liber quadratorum»/«Квадраттар кітабы», 1225 — белгісіз квадрат теңдеулер жайындағы есептер) түрлі-түрлі математикалық есептерді өте жиі талдап отырды.  

Фибоначчидің өзінің өмірлік жолы туралы мағлұмат өте мардымсыз. Бірақ оның есептері келесі ғасырларда математиктер арасында өте танымал болғаны анық. Қазір сол есептердің бірін қарастырып көрмекпіз.  

Фибоначчидің қояндар жөніндегі есебі

Есепті орындау үшін автор мына шарттарды қойды: еркек және ұрғашы болған жаңа туған екі көжек бар, өмірінің екінші айында дүниеге жаңа екі көжек әкеледі (еркек және ұрғашы). Солай көбие береді. Қояндар шектеулі кеңістікте жүреді және үнемі туып көбейіп отырады. Бірде бір қоян өліп қалмайды.   

Есеп: бір жыл өткенде қояндар саны қанша болатынын анықтау.   

Шешімі:

Бізде бары мынау:

— Бірінші айдың басында бір қояндар жұбы бар, олар айдың соңында шағылысады

— Екінші айда екі қояндар жұбы бар (бірінші жұп және бірінші жұптың тұқымы)

— Үшінші айда үш қояндар жұбы бар (бірінші жұп, бірінші жұптың ұрпағы және жаңа туған ұрпағы)  

— Төртінші айда бес қояндар жұбы бар (бірінші жұп, бірінші жұптың бірінші және екінші ұрпағы, бірінші жұптың үшінші ұрпағы және екінші жұптың бірінші ұрпағы)  

Бір айдағы қояндар саны «n» = өткен айдағы қояндар саны + жаңа қояндар жұптарының саны, басқаша айтқанда жоғарыда айтылған формула: Fn = Fn-1 + Fn-2. Бұдан рекурренттік (рекурсия жайында төменіректе айтамыз) сандар тізбегі шығады. Бұл жердегі әр бір жаңа сан алдындағы екі санның қосындысына тең.  

1 айда: 1 + 1 = 2

2 айда: 2 + 1 = 3

3 айда: 3 + 2 = 5

4 айда: 5 + 3 = 8

5 айда: 8 + 5 = 13

6 айда: 13 + 8 = 21

7 айда: 21 + 13 = 34

8 айда: 34 + 21 = 55

9 айда: 55 + 34 = 89

10 айда: 89 + 55 = 144

11 айда: 144 + 89 = 233

12 айда: 233 + 144 = 377

Және де бұл тізбек шексіз түрде ұзақ жалғасып кете беруі мүмкін, бірақ, мақсатымыз бір жыл өткен кездегі қояндар санын білу болғандықтан, 377 жұп шығып отыр.    

Бұл тұста, егер бірінен кейін бірі келетін екі сандар жұбын салыстырып, үлкен санды кішісіне бөлсек, шығатын нәтижесі алтын қимаға қарай жылжып отыратыны Фибоначчи сандарының қасиеттерінің бірі болып табылатынын ескерте кету де маңызды. Алтын қима туралы да төменде айтып өтеміз. 

Оған дейін сіздерге Фибоначчи сандары бойынша  тағы екі есепті ұсынамыз:  

— Одан 5-ті алып тастаса немесе оған 5-ті қосса, тағы да квадрат сан шығатыны ғана белгілі квадрат санды анықтау.  

— 7-ге бөлінетін санды, алайда есеп шарты бойынша ол санды 2-ге, 3-ке, 4-ке, 5-ке және 6-ға бөлгенде қалдығы 1 болатын санды анықтау.  

Бұндай есептер ақыл-ойды дамытудың керемет тәсілі ғана емес, сондай-ақ уақытты қызықты өткізудің де жақсы амалы. Бұндай есептердің қалай шығарылатыныны жөніндегі ақпаратты сіздер Интернеттен іздеп тауып алуларыңызға болады. Біз болсақ, оған көңіл аударып жатпастан, өз әңгімемізді жалғастырайық.  

Рекурсия және алтын қима дегеніміз не нәрсе?  

Рекурсия

Рекурсия қандай да бір нысанның немесе үдерістің сол нысанның немесе үдерістің өзі бар сипаттамасы, анықтамасы немесе бейнесі болып табылады. Басқаша айтқанда, нысанды немесе үдерісті өзінің бір бөлігі деп атауға болады.    

Жалпы мағынасында рекурсия — элементтерін өзіне ұқсас түрде қайталайтын процестер.

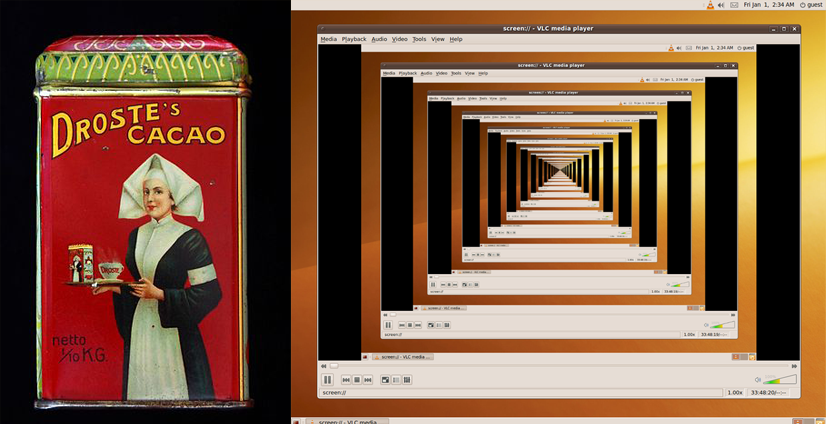
Рекурсия математикалық ғылымда ғана емес, сонымен қатар информатикада, бұқаралық мәдениетте және өнерде барынша қолданылады. Фибоначчи сандарына қатысты айтсақ, егер «n>2» болса, онда «n» = (n-1)+(n-2) болады.  

Алтын қима

Алтын қима (алтын қатынаc) жалпы шаманың үлкен бөлігіне қатынасатыны сияқты үлкеннің кішіге қатынасы қағидаты бойынша бүтіннің бөлшектерге бөлінуі болып табылады.

Ең алғаш рет алтын қима жайында дұрыс үшбұрышты құру туралы айтатын Евклидтің еңбектерінде жазылған («Бастама» трактаты, шамамен б.д. дейінгі 300 жыл). Алайда бізге үйреншікті болып кеткен ұғымды неміс математигі Мартин Ом енгізген болатын.    

Шамалап алғанда алтын қиманы екі әрқилы бөліктерге пропорционалды түрде бөлу ретінде көзге елестетуге болады. Мысалы, 38% те 68%. Алтын қиманың сандық өрнегі шамамен 1,6180339887 тең болады.   

Іс жүзінде алтын қима сәулет өнерінде, бейнелеу өнерінде (Леонардо да Винчидің еңбектерін қарап шығыңыз), кинода және басқа салаларда пайдаланылады. Ұзақ уақыт бойы, тіпті қазіргі кезде де, алтын қима эстетикалық пропорция болып саналып келді, дегенмен адамдардың көпшілігіне ол бейпропорционалды — сопайып созылған сияқты болып көрінеді.  

Сіз, мына пропорцияларды басшылыққа ала отырып, өзіңіз алтын қиманы бағамдап көре аласыз:

— a кесіндісінің ұзындығы = 0,618

— b кесіндісінің ұзындығы = 0,382

— c кесіндісінің ұзындығы = 1

— c мен a арақатынасы = 1,618

— c мен b арақатынасы = 2,618

Енді алтын қиманы Фибоначчи сандарына қолданып көрейік: оның тізбегіндегі екі көршілес мүшесін алып, олардың үлкенін кішісіне бөлеміз. Шамамен 1,618 шығады. Ал егер де тізбектегі сол үлкен санды алып, өзінен кейін тұрған үлкен санға бөлсек, шамамен 0,618 шығады. Өзіңіз есептеп көріңіз: 21 және 34 сандарымен немесе басқа сандармен «ойнаңыз». Егер Фибоначчи тізбегінің алғашқы сандарымен осы тәжірибені жасап көрсеңіз, бұндай нәтиже шықпайды, өйтетін себебі, алтын қима тізбектің бас жағында «іске жарамай қалады». Айтпақшы Фибоначчидің барлық сандарын анықтап алу үшін бірінен кейін бірі тұратын үш санды білу жеткілікті.  

Сөз соңында тағы біраз ақылға азық болар мәлімет берейік.  

Алтын тіктөртбұрыш және Фибоначчидің шиыршығы

«Алтын тіктөртбұрыш» — бұл тағы бір алтын қима мен Фибоначчи сандарының арасындағы өзара байланыс, өйткені оның қабырғаларының арақатынасы 1-ге 1,618 болады (1,618 санын есіңізге түсіріңіз!).  

Мынау соның мысалы: Фибоначчи тізбегіндегі екі санды, мысалы, 8 бен 13 сандарын, аламыз және ені 8 см, ал ұзындығы 13 см болатын тіктөртбұрышты сызамыз. Сосын негізгі тіктөртбұрышты кішіректеріне бөлеміз, бірақ олардың ұзындықтары мен ендері Фибоначчи сандарына сәйкес келуі тиіс — үлкен тіктөртбұрыштың бір қырының ұзындығы кіші тіктөртбұрыштың қырының екі ұзындығына теңесуі тиіс.    

Осыдан кейін бізде бар барлық тіктөртбұрыштардың бұрыштарын біртіндеп бұрылатын сызықпен жалғаймыз да, логорифмдік шиыршықтың дара жағдайын — Фибоначчи шиыршығын аламыз. Оның негізгі қасиеттері шекараларының жоқтығы және пішінінің өзгеруі болып табылады. Бұндай шиыршықтар табиғатта жиі кездесіп тұрады: ең жарқын мысалдарына ұлулардың қабыршағы, жерсеріктен түсірілген суреттерде бейнеленген циклондар және тіпті бірқатар галактикалар жатады. Бірақ бәрінен қызығы — тірі организмдердің ДНҚ да осы ережеге бағынады, оның пошымы шиыршық тәрізді екенін ұмытпаған боларсыз?    

Осы және басқа «кездейсоқ» сәйкестіктер қазіргі күндері де ғалымдардың ойын онға бөліп, 18 мың Ғаламдағының бәрі бір алгоритмге, нақтырақ айтсақ математикалық алгоритмге бағынып тұр деген ойға қалдырады. Ал бұл ғылым болса, өзінде әлі ұшан-теңіз құпиялар мен жұмбақтарды бүгіп жатыр. 

---

Әлеуметтік желілерде бөлісіңіз: