Квадрат теңдеу және оның түбірлері

Қызылорда обылысы,

Жаңақорған ауданы,  №180 «Қызылмақташы»

орта мектебінің математика пәні мұғалімі

Таласбаева Меруерт Жалдықарақызы

8-сынып. Алгебра

Модуль сабақ: «Квадрат теңдеу және оның түбірлері»

Мақсаты. Квадрат теңдеуді  шешу тәсілдерімен таныстыру,  есеп шығаруда нақты, қажетті  тәсілдерін  таңдай білуге үйрету.

Логикалық  ойлауын, есте сақтауын, зейінін  дамыту.

Еңбексүйгіштікке, ұйымшылдыққа, математикалық мәдениетке тәрбиелеу.

 

Модуль құрылымы:

Барлығы -7 сағат

Кіріспе бөлімі -1 сағат

Сөйлесу бөлімі - 5 сағат

Қорытынды бөлімі -1 сағат

Міндеттері:

А) Білімдік - сабақ барысында оқушылардың квадрат теңдеулерді шешуін бекіту, қайталауын, білімдерін тереңдетуін қамтамасыз ету.

Б) Дамытушылық - білім дағдысын  практикада пайдалана білуге, оқулықпен өздігінен жұмыс жасау дағдысын   және іскерлігін қалыптастыру, тапқырлыққа баулу.

В) Тәрбиелік - ұжымшылдыққа баулу, ұйымшылдыққа, ұқыптылыққа тәрбиелеу, еңбек ете білуге машықтандыру.

ЛЕКЦИЯ

3х+х²=0, -3х²+2х-5=0,  2х²-7=0, х²-9х=0, 5х²=0 түріндегі теңдеулер квадрат теңдеулер деп аталады.

Анықтама.  aх²+вх+с=0 (мұндағы х-айнымалы, а,в,с-қандай да бір сандар,а≠0 ) түріндегі  теңдеу квадрат теңдеу деп аталады.

 а,в,с-коэффициенттер, а-І, в-ІІ, с-бос мүше деп аталады.

Егер aх²+вх+с=0  квадрат теңдеуінде в немесе с  коэффициенттерінің  бірі 0-ге тең болса, мұндай теңдеу  толымсыз квадрат теңдеу деп аталады.

 Х²-6х=0, 3х²=0,  -4х²+12=0

Толымсыз квадрат теңдеу үш түрде болады:

1) aх²+с =0;    с≠0

2)  aх²+вх=0; в≠0

3)   aх²=0

х²+вх+с=0 түріндегі теңдеу, яғни а=1 болса,   келтірілген квадрат  теңдеу деп аталады.

Мұндай теңдеу  квадрат екімүшені айыру тәсілімен  шығарылады.

 

.  aх²+вх+с=0 квадрат теңдеудің  түбірін  табу формуласы:

                                                    -b±√D

1) егер D>0 болса,  онда х_1/2 =      ----------, мұндағы   D=b²-4ac,

                                                       2а                                              

                            

 

                                        D

 

2) егер D=0, онда  х=       -----

                                       4а²

 

 

3) егер  D<0,    теңдеудің түбірі жоқ

 

Квадрат  теңдеуді формула бойынша  шешуде мыналарды қолданамыз:

1. Дискриминантты есептеу және оны нөлмен салыстыру.
2. егер дискриминант  оң сан болса немесе нөлге тең болса, онда формуланы пайдаланамыз, ал дискриминант  теріс сан болса, онда түбірі жоқ деп жазамыз.

 

Квадрат теңдеу көмегімен  математика, физика, техникада көптеген есептер шығарылады.

Квадрат теңдеудің  түбірлерін  Виет  теоремасы  бойынша  да табуға болады.

Виет теоремасы: Келтірілген квадрат теңдеудің  түбірлерінің  қосындысы  қарама-қарсы таңбамен алынған  екінші коэффициентке, ал көбейтіндісі  бос мүшеге тең болады:

                   х₁+х₂ =-в, х₁ х₂=с 

aх²+вх+с=0 квадрат теңдеудің түбірлері х₁ , х₂ болса, оған мына келтірілген теңдеу мәндес теңдеу болады:   

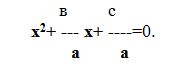
Виет теоремасы бойынша :   х₁+х₂ = -в/а;   х₁ х₂=с/а

Бекіту сұрақтары:

1. Квадрат теңдеу  анықтамасы.
2. Квадрат теңдеу коэффициенттерін  ата.
3. ТОлымсыз квадрат теңдеу  дегеніміз не?
4. Толымсыз квадрат теңдеуге әр түрлі  мысалдар келтір.
5. КЕЛТІРІЛГЕН КВАДРАТ ТЕҢДЕУ ДЕГЕНІМІЗ НЕ?
6. Квадрат теңдеудің түбірін табу формуласын  жаз.
7. Дискриминант қандай формуламен есептеледі?
8. Квадрат теңдеуді шешу  алгоритмін айт.
9. Виет теоремасын тұжырымда.
10.  Квадрат теңдеуді келтірілген квадрат теңдеуге қалай келтіреміз?

С/р	Оқу материалдары	Оқушы әрекеті
кіріспе	Мақсаты: Өздігінен жұмыс істей білуге үйрету, жұп бойынша жұмыс орындаттыру, сұрақтар қою арқылы  жаңа материалды бекіту, әр түрлі теңдеулерді шешу  іскерлігін қалыптастыруды ұйымдастыру.
Сөйлесу бөлімі-1	Мақсаты: Квадрат теңдеуді  шешу тәсілдерін  меңгеру дағдысын  қалыптастыру,  квадрат теңдеудің типтерін  ажырата білу және оны шешу тәсілдерін игерту.
	Нұсқаулық карта № 1:  1. Теңдеу анықтамасын айт.	Оқулықпен жұмыс
	2. Теңдеуді шеш	(№1 топтамадан №1)
	3. Квадрат теңдеу анықтамасын айт	Оқулық, 51-бет
	4. Берілген теңдеуді квадрат теңдеу түріне келтіруге бола ма?   А) Егер болса,  теңдеуді квадрат теңдеуге келтір. Б) Берілген  теңдеудің  коэффициенттерін ата. В) Мына түрдегі  теңдеу қалай аталады? Г) Пайда болған теңдеудің бірін таңда   Д) Алгоритм бойынша есепті шығар	А) Мысалдар келтіру  Б) Дәптерге коэффициенттерін жазу В) Оқулық,64-бет Г) Дәптерге көшіріп, оны екі мүшенің  квадратын айыру тәсілімен шеш Д) №1 топтамадан №2 тапсырма
	5. Қандай теңдеуді толымсыз квадрат теңдеу деп атайды?	Оқулық, 51-бет
	6. Әр түрдегі толымсыз квадрат теңдеуге мысал келтір.	Жұптық жұмыс
	7. Әртүрлі толымсыз квадрат теңдеудің неше түбірі болады? 8. теңдеулерді шешіңдер.	Ауызша   №2 топтамадағы  №1,2,3,4,5,6 (әркім өз бетінше орындайды дәптерге)
2-ші сабақ	Квадрат теңдеуді шешуді  формула бойынша  орындау
	Нұсқаулық карта №2: 1.Квадрат теңдеудің  дискриминанты деген не? Квадрат теңдеудің неше түбірі болуы мүмкін.	Оқулық, 56-57 беттер
	2. Квадрат теңдеудің түбірін табу формуласын жазу.	Дәптерге орындау
	Коэффициенттері жұп сан болғандағы  квадрат теңдеудің  түбірін табу формуласын жаз.	Оқулық,59-бет
	Формула бойынша квадрат теңдеуді шешу жоспарын құр.	Ауызша. Жоспарды дәптерге жазу.
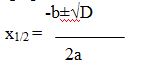
	5. Дәптерге орындау: теңдеуді шеш: 2х2+х-21=0 а=2, в=1,с=-21 Формула бойынша дискриминантты табамыз: D=b2-4ac D=1-4*2*(-21)=1+168=169=132, D>0 Формула бойынша теңдеу түбірін табамыз:          х1=(1-13)/4 =-3,  х2 =(1+13)/4=3,5   Жауабы: -3; 3,5.	№3 топтамадағы тапсырманы орында.
3-ші сабақ	Мақсаты: Квадрат теңдеуді шешу дағдысын одан әрі қалыптастыру.Есеп шарты бойынша теңдеу құра білуге машықтандыру. Есеп шарты мен  табылған шешімінің сәйкестігін  тексере білуге үйрету
	Нұсқаулық карта№3: 1. Оқулықтағы текстпен өздігінен жұмыс жасай білуге , ең бастысын  анықтай білуге үйрету.	62-63 беттегі 12 пунктті оқу
	2. 62-63 беттегі 1-2 тапсырма шешуін қарастыру.	Дәптерге  62-63 беттегі 1-2 тапсырма шешуін жазу.
	3. Есеп шартымен таныстыру	№4 топтамадағы есепті шешу үшін теңдеу құру.
4—ші сабақ	Мақсаты: Формула бойынша квадрат теңдеуді шешу дағдысын тереңдету.
	Франсуа  Виет туралы хабарлама даярлау. №4 топтама бойынша тапсырма  орындау.	Үйге тапсырма: Франсуа Виет туралы  тарихи анықтама құрастыру; №4  топтамадағы қалған тапсырмалар ды орындау
5-ші сабақ	Мақсаты:Келтірілген квадрат теңдеудің коэффициенттері  мен түбірлерінің арасындағы тәуелділікті «ашу».Виет теоремасын және оған кері  теореманы қолдана білуге үйрету. Виет өмірінен мысал келтіре отырып,  оқушының математикаға қызығушылығын арттыру.
	Нұсқаулық карта №4: Кестені толтыр: теңдеу Х1 және х2 түбірлері                    х1+х2                    х1 х2	Формула бойынша келтірілген квадрат теңдеуді шешу (№5 топтама)
6-шы сабақ	Мақсаты: Оқушылардың алған білімдерін  қолдана білу іскерліктерін қалыптастыру.
	Нұсқаулық карта №5: 1. Келтірілген квадрат теңдеудің коэффициенттері  мен түбірлерінің арасындағы  заңдылықты анықта.	Оқулық, 64-бет
	2. Виет теоремасын дәлелдеу	Оқулық, 65-бет
	3. Кері теоремасын айтып беру.	Ауызша
	4. Виет теоремасына кері теореманы дәлелдеңдер.	Жұптық жұмыс
	5. Квадрат теңдеудің түбірі  дұрыс табылғандығын тексеріңдер.	Дәптерге жазу
	6. Теңдеу түбірін таңдаңдар.	№6 топтамадағы №1 тапсырма
	7. Соңғы теңдеудің  бастапқы теңдеуден ерекшелігін  анықтаңдар. 8. aх2+вх+с=0 квадрат теңдеудің түбірлерінің көбейтіндісі мен қосындыысы неге тең?	Дәптерге жаз.   №6 топтамадағы №2 тапсырманы орындап дәптерге жаз.
	9. Теореманы есте сақтау үшін  өлең шығар	Дәптерге жазып, жаттап ал
	10. Үйге тапсырма: Шығармашылық тапсырма.	1. Мына теңдеулерді шешу тәсілін тап: ax2=bx, ax2=c, ax2+c=bx, ax2+bx=c6 bx+c=ax2 `a,b,c әріптері оң сандар, VII ғасыр) 2.  1591 жылы теңдеу түбірлерінің оның коэффициенттеріне тәуелділік  формуласы қандай түрде болды?
7-ші сабақ	Мақсаты: Квадрат теңдеулерді шешудегі білім-білік дағдыларын тексеру.
Қоры тынды	Нұсқаулық карта №6: Бақылау жұмысы                       І нұсқа 1. Теңдеуді шешіңдер: а)  5х2+8х-4=0           в) 6х2=18х б) 25х2-4=0     г) (х+3)2-2(х+3)-8=0   2. Көбейтіндісі 132-ге тең болатын тізтектес екі натурал сандарды тап.   х2-4х+с=0 квадрат теңдеуінің бір түбірі 2+√3.  2-ші түбірін және с мәнін тап.                 ІІ нұсқа   1. Теңдеуді шешіңдер: а)  5х2+14х-3=0          в) 4х2=16х б) 36х2-25=0   г) (х-3)2-2(х-3)-15=0   2. Екі натурал санның бірі екіншісінен  3-ке артық. Олардың  көбейтіндісі 180-ге тең болса осы  сандарды тап.   х2-х+q=0 квадрат теңдеуінің  түбірлері 3х1+2х2=0 шартын қанағаттандырады. q  мәнін тап.	Әр оқушы өз бетінше жұмыс жасайды

 

Ойындар.

1 – ойын «Байқап қал»  

Бұл ойынға балалар 2топқа бөлініп қатысады. 2топ өздеріне басшылар тағайындап алады. Олар стол үстіне 10 – 15 ұсақ нәрселерді қойып, (мысалы, формулалар жазылған, фигуралар салынған қималар) балаларға 1минут қаратқаннан кейін өздері көрген нәрселердің тізімін жазуларын тапсырады. Қай топтың балалары көп жазса, сол топ ұтқан болып саналады. Ойын көру, ойда сақтау қабілеттерін жетілдіре түседі.

2 – ойын    «Арқан тартыс»    Оқушылар 2 топқа бөлінеді. Тақта алдына ұзын жіп байланады. Киіз үй жиһаздары, ұлттық киімдер зергерлік бұйымдар т.б. суреттер салынған конверттер ілінеді. Әрбір оқушы өзіне ұнаған конвертті қиып алып, оның ішіндегі сұраққа жауап береді , есептер шығарады. Топтағы оқушылар бір – біріне көмектеседі. Қай көп тапсырма орындаса сол топ жеңеді. Ойын ұжымдық іс- әрекетке тәрбиелейді.

Бұдан басқа да «Орамал тастау», «Жүйріктер жеңеді», «Дәлдеп көзде», «Жорға», «Кім тапқыр?», «Көкпар» ойыны т.б. ойындар ойнатуға болады.

Жұмыс дәптерінен

«Квадрат теңдеу» тақырыбына  деңгейлік тапсырмалар

І деңгей

1. Коэффициенттерін ата:  3х+х²=0, -3х²+2х-5=0,  2х²-7=0, х²-9х=0, 5х²=0

2. Толымсыз квадрат теңдеуге бірнеше мысал келтір

3. D-ын есепте: 3х²+2х-5=0

4.Виет теоремасын айт

ІІ деңгей

1. теңдеуді шеш:

2х²+х-21=0

2. теңдеуді шеш:

      3х²+х=0

3. Теңдеуді шешіңдер:

 6х²=18х

4.  Теңдеуді шешіңдер:

 25х²-4=0   

ІІІ деңгей

1.  Теңдеуді шешіңдер:

 (х+3)²-2(х+3)-8=0

2. Көбейтіндісі 132-ге тең болатын тізтектес екі натурал сандарды тап.

IV деңгей (шығармашылық)

1. х²-4х+с=0 квадрат теңдеуінің бір түбірі 2+√3.

 2-ші түбірін және с мәнін тап.

 

2. Бір шырпыны жылжыту арқылы теңдік тура болатындай ету керек: XI+I=X? Неше шешімі бар?

---