Кәлтүрүш формулилири

Алматы облысы, Ұйғыр ауданы
"Долайты орта мектебі" КММ-сінің
математика және физика пәні мұғалімі  
Даутова Махирям Телебалдыевна

 

9"ә" синип                                    Алгебра                                                                                     

Дәрис мавзуси: Кәлтүрүш формулилири

Дәрис мәхсити: кәлтүрүш формулилирини чүшәндүрүш; оқуғучиларниң есап чиқириш маһаритини ашуруш; оқуғучиларни уюшчанлиққа, коллективлиқ тәрбийләш.

Дәрисниң типи: йеңи билимни өзләштүрүш.

Дәрисниң усуни: чүшәндүрүш, соалға–жавап.

Пәнләр ара бағлиниши: тәбиәт, уйғур тили.

Көрнәклик қурал: таблица, карточкилар.

Қолланған әдәбийәт: алгебра. 9-синип. А.Әбилқасымова, И.Бекбоев,А.Абдиева, З.Жумағулова

Дәрисниң бериши.

І. Уюштуруш.

ІІ. Өй тапшурмисини тәкшүрүш

§18. №290

ІІІ. Өткән материаллар бойича тәкрарлаш.

1. Еғизчә һесап
2. Карточка билән иш

ІV. Нәтижиләш.

Оқуғучиларниң жавави бойичә йәкүнләймән.

V.  Йеңи материалға чүшүнүк.

Мәзкүр мавзуни оқуш ж,әриянида силәр немини үгинисиләр?

Берилгән мавзуни өзләштүрүп,тар булуңниң тригонометриялик функциясиниң һәр бир булуңдики синусниң, косунусниң, тангенсниң, котангенсниң кәлтүрүш формулилири билән тонушуп, мошу формулиларни  тригоно­метриялик ипадиләрни түрләндүрүштә вә һесапларни чиққарғанда қоллинишни үгинисиләр.

Тригонометриялик функцияләр билән бағлиқ, көплигән һесапларни чиқарғанда тригонометриялик функцияниң халиған булуңини тригонометриялик функцияләрниң тар булуңиға кәлтүрүшниң әһмийити зор. Башқичә ейтқанда, әгәр 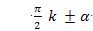 (бу йәрдики k - хали­ған пүтүн сан, α - тар булуң) булуңиниң функциялири берилсә, у чағда уларни α булуңиға бағлиқ тригонометриялик функцияләргә кәлтүрүш колайлиқ. Униң үчүн мәхсус берилгән кәлтүрүш формилилири қоллиниду.

Биз пәқәт бәзи бир hаләтләрдила қоллинилидиған кәлтүрүш формулилирини k = 1; 2; 3; 4 болған hаләттә, 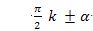 ипадисини, йәни  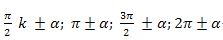булуңлири үчүн қараштуримиз.

Башқа булуңлар (k ниң пүтүн мәнасиниға мувапиқ, қалған булуңлар) жуқурида көрситилгән пүтүн булуңларниң миқдарлириға 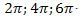  вә ш. о. қошуш йоли билән елиниду.

Алди билән, синус вә косинус үчүн кәлтүрүш формулилирини қараштурайли. Андин улар арқилиқ тангенс вә котангенс үчүн  кәлтүрүш формулилирини оңай чиқиришқа болиду.

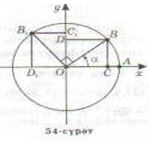ІІ чарәктики синус вә косинус үчүн кәлтүрүш формулилирини чиқирайли. ІІ чарәктики һәр бир булуңни  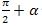түридә кәлтүрүшкә болиду (бу йәрдики α-тар булуң). Чәмбәр алайли, О чекитини айлaндуруп чәмбәрниң R = ОА радиусини α булуңиға бурайли, андин 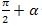булуңиға йәнә бураймиз (54-сүрәт). Мошу бурашлар ж,әриянида ОА радиуси мувапиқ ОВ вә ОВ₁ радиусиға авушиду. В вә В₁ чекитлиридин координатилиқ оқларға перпендикуляр жүргүзимиз. Нәтиж,идә, OCBD вә OC₁B₁D₁ икки тик төртбулуңлуқ алимиз. OC₁B₁D₁  тик төртбулуңлуғи О чекитини айландуруп OCBD тик төртбулуңлуғини иж, абий йөнилиштә  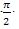булуңиға бураш арқилиқ чиқти. Һәқиқәтән,  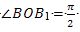болғанлиқтин, бураш ж,әриянида В чекити В₁ чекитигә көчиду. Дәл мошундақ С чекити С₁ чекитигә, D чекити D_j чекитигә көчиду.

Шуниң үчүн В₁ чекитиниң ординатиси ретидә В чекитидики абсциссини елишқа болиду, В₁ чекитиниң абсциссиси ретидә В чекитиниң ординатисини қариму-қарши тамға билән елишқа болиду:                                       

                               у₁=x   вә   х₁= - y                       

яки

                          

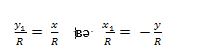
Ениқлима бойичә булуңниң синуси ординатиниң радиусқа нисбитигә тәң екәнлигини билимиз, йәни

 

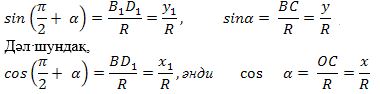
Берилгәнләрни әскә елип, кейинки тәңликләрдин төвәндикини алимиз:

 

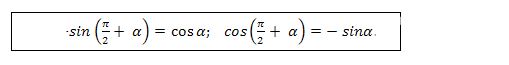(1)

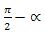 булуңи үчүн синус вө косинусниң  кәлтүрүш формулилирини чиқириш үчүн (1) формулидики α булуңини - α булуңиға авуштурса йетәрлик, шунда

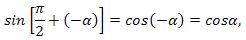
чүнки косинус функцияси жүп;

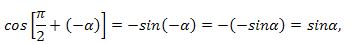
чүнки синус функцияси тағ.

Шуниң билән йәнә икки кәлтүрүш формулисини чиқиримиз:

Мошу икки формула α тар булуңи үчүнла әмәс, халиған α булуңи үчүнму һәқиқий, Әнди 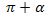 булуңи үчүн синус вә косинусқа кәлтүрүш формулилирини чиқирайли.

Униң үчүн 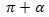 булуңини  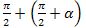түригә кәлтүрүп, (1) формулини икки қетим қоллинимиз, шунда

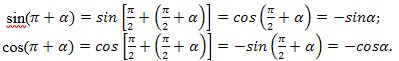
Яки                                

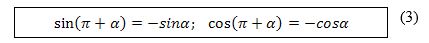
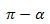        булуңини  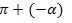түригә кәлтүрүп, (3) формулидин 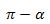булуңиниң синус вә косинусини тeпишка болиду:

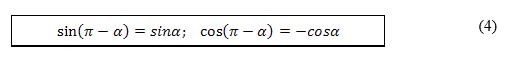
(4) формулиниң һәқикийлигини мустәкил испатлаңлар.

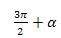 булуңи үчүн синус вә косинусниң кәлтүрүш формулилири чиқиримиз. Бу йәрдә (З) формулини алғанда колланған усулни пайдилинимиз, башқичә ейтқанда,  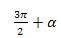булуңини  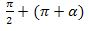түригә кәлтүримиз. Униңдин кейин (1) вө (3) формулилирини пәйдин-пәй коллансақ,

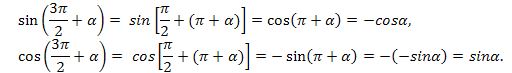
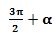       булуңи үчүн синус вә косинусниң кәлтүрүш формулилирини мустәқил испатлаңлар.

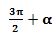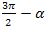        вә  булуңлири үчүн синус вә косинусниң кәлтүрүш формулилирини айрим язайли:

     

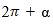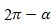Әнди  вә   булуңлири үчүн синус вә косинусниң кәлтүрүш формулилирини чиқирайли. Алди билән 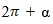булуңи үчүн кәлтүрүш формулилирини қараштуримиз. Әгәр α булуңиға (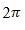) толуқ булуңини кошсақ, униңдин тригонометриялик функцияләрниң мәналири өзгәрмәйду (§ 16).

Шуниң үчүн

           

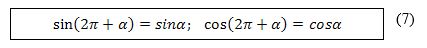
Әнди (7) формулидики α булуңини -α булуңиға алмаштуримиз:

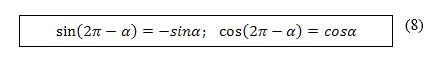
(8) формулиниң испатлимисини өэәңлар көрситиңлар.

Жуқурида испатланған (1) вә (8) формулилири асасида   формулисини қоллинип, тангенс вә котангенсқа кәлтүрүш формули­лириниң һәқикийлигини мустәқил испатлаңлар:

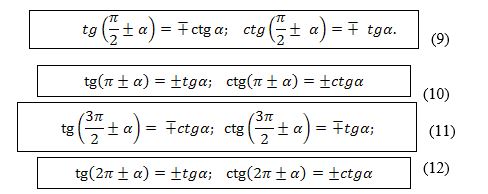
Барлиқ кәлтүрүш формулилирини бир ж,әдвәлгә киргүзәйли:

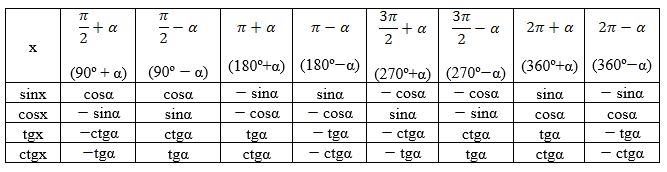
Мошу ж,әдвәлдин қандақ канунийәтни байқашқа болиду?

Ж,әдвәлни қоллинип, келәси соалларға жавап берип көрүңлар:

1. Қандақ hаләттә функция өзгәрмәйду?
2. Қайси вақитта синус косинусқа, тангенс котангенсқа вә әксичә косинус синусқа, котангенс тангенсқа авушиду?
3. Кәлтүрүш формулисиниң иж,абий тәрипидики функцияниң тамғисини қандақ ениқлашқа болиду?

Мошу параграфта ейтилғанларни хуласиләйли:

-    әгәр кәлтүрүлгән тригнометриялик функцияниң аргументи (булуңи)
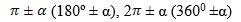-  түридә болса, у чағда униң нами өзгәрмәйду;
-    әгәр кәлтүрүлгән тригонометриялик функцияниң аргументи (булуң)
түридә болса, у чағда синус косинусқа, косинус синусқа, тангенс котангенсқа, котангенст ангенсқа өзгириду;
-    кәлтүрүш формулисиниң оң тәрипиниң тамғиси мувапиқ чарәктики кәлтүрүлгән функцияниң тамғиси билән бирдәк йезилиду.

1-мисал. 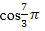  мәнасини тапайли.

Йешиш.

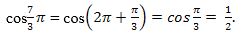
2-мисал.sin(–780º) мәнасини һесаплайли.

Йешиш. sin(–780º)=  –sin780º= –sin(2٠360º + 60º) =  –sin60º =  –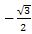

 

3-мисал.tg(–1110º) мәнасини тапайли.

Йешиш. tg(–1110º) = – tg1110º = –tg(3٠360º+30º) = –tg30º= – .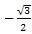

4-мисал.  a) ctg1665º; 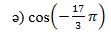    мәналирини һесаплайли.

Йешиш. a) ctg1665º = ctg(4٠360º + 225º) = ctg225º = ctg(180º+45º)  = ctg45º = 1

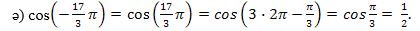
5-мисал.

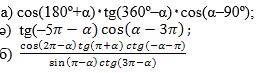  ипадилирини ихчамлайли.

Йешиш.

 

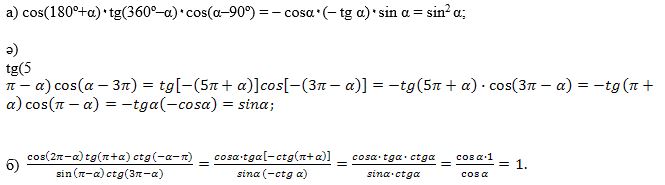
VI. Һесап чиқириш

VІІ. Нәтижиләш. Оқуғучилар чиқарған һесаплири бойичә йәкунләймән.

VІІІ. Өйгә тапшурма.

---