Ипадиләрни түрләндүрүштә асасий тригонометриялик тәңму-тәңликләрни қоллиниш

Алматы облысы, Ұйғыр ауданы
"Долайты орта мектебі" КММ-сінің
математика және физика пәні мұғалімі  
Даутова Махирям Телебалдыевна

 

9"ә" синип  Алгебра                                                                                     

Дәрис мавзуси: Ипадиләрни түрләндүрүштә асасий тригонометриялик тәңму-тәңләрни қоллиниш

Дәрис мәхсити: Тригонометриялик функцияләрниң хусусийәтлирини чүшәндүрүш; оқуғучиларниң есап чиқириш маһаритини ашуруш; оқуғучиларни уюшчанлиққа, коллективлиқ тәрбийләш

Дәрисниң типи: йеңи билимни өзләштүрүш

Дәрисниң усуни: чүшәндүрүш, соалға – жавап.

Пәнләр ара бағлиниши: тәбиәт, уйғур тили.

Көрнәклик қурал: таблица, карточкилар

Қолланған әдәбийәт: алгебра. 9-синип. А.Әбилқасымова, И.Бекбоев,А.Абдиева, З.Жумағулова

Дәрисниң бериши.

І. Уюштуруш.

ІІ. Өй тапшурмисини тәкшүрүш

§18. №290

ІІІ. Өткән материаллар бойича тәкрарлаш.

1. Еғизчә һесап
2. Карточка билән иш

ІV. Нәтижиләш.

Оқуғучиларниң жавави бойичә йәкүнләймән.

V.  Йеңи материалға чүшүнүк.

Мәзкүр мавзуни оқуш ж,әриянида силәр немини үгинисиләр?

Бу мавзуни өзләштүрүп, тригонометриялик ипадиләрни mәңму-тәң түрләндүрүшни вә тригоно­метриялик тәңму-тәңликләрни испатлашни үгинисиләр.

Бир аргументқа бағлиқ тригонометриялик функцияләрниң ариси­дики нисбәтни ипадиләйдиған формулиларни биз өткән параграфта қараштурдуқ. Шуниң билән биллә тригонометриялик функцияләр­ниң мәналирини берилгән бир мәнаси бойичә ениқлаш вақтида мошу формулиларни қоллинишқа мисал қараштурдуқ. Бу формулилар ипадилар ипадиләрни ихчамлаш вә тәңму-тәңликләрни испатлаш мәхситидиму коллинилиду.

1-мuсал. cоs²α+1+ sin²α ипадисиниң мәнасини тапайли.

Йешиш. Униң үчүн §19 дики (1) формулини коллинайли. Шунда cos²α + 1 + sin²α = (cos²α + sin²α)+1=1+1=2          Жавави: 2.

2-мисал. 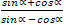   кәсирини  tgα арқилиқ ипадиләйли.

Йешиш. Униң үчүн 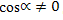 дәп елип, кәсирниң мәхриж,и вә сүритиниң һәр қошулғучини соsα ға бөләйли. Шунда

3-мисал. 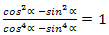  тәңму-тәңлигини испатлаңлар.

Испатлаш: Мәхриж,идики ипадигә икки ипадиниң квадратлириниң айрими формулисини қоллинимиз. Шунда

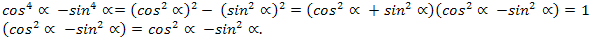
Демәк

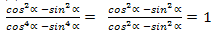
Берилгән мисалда теоремини испатлаш үчүн тәңму-тәңликнин сол тәрипини түрләндүрүп, оң тәрипини чиқардуқ.

Бәзидә әксичә оң тәрипини түрләндүрүп, сол тәрипини чиқириду.

4-мисал. 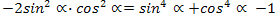тәңму-тәңлигини испатлайли.

Исnаmлаш. Униң үчүн тәңму-тәңликниң оң тәрәп бөлигигә 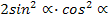  ипадисини қошуп вә кемитәйли. Шунда,  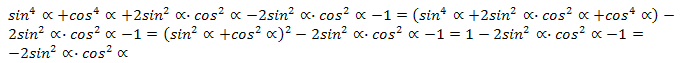 алимиз.

Бәзи һаләтләрдә тәңму-тәңликни испатлаш үчүн тәңму-тәңликниң һәр иккила бөлигини түрләндүрүш керәк.

5-.мuсал. 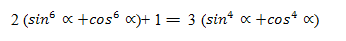тәңму-тәңлигини  испатлайли.

Исnаmлаш. Алди билән сол тәрәп бөлигидә турған ипадини түрләндүрәйли.

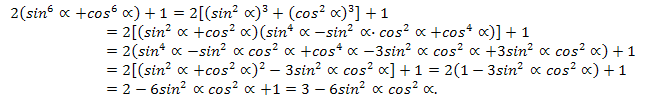
Әнди тәңликниң иж,абий тәрипидә турған ипадини түрләндүрәйли.

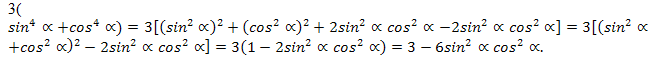
Шуниң билән, тәңму-тәңликниң һәр иккила бөлигини түрләндүрүп, бирдәк 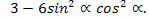  ипадисини алдуқ. Демәк, тәңму-тәңлик испатланди. Бәзи һаләтләрдә тәңму-тәңликләр математикилиқ операцияләрни әмәлгә ашуруш йоли биләнму испатлиниду.

6-мисал. 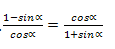тәңму-тәңлигини испатлайли

Испатлаш. Бу тәңму-тәңликни пропорция  ретидә қараштурушқа болиду. Пропорцияниң хусусийити бойичә (1– sinα)(1+sinα)=cosα

Һәқиқәтәнму (1– sinα)(1+sinα)=1–sin²α = cos²α

 Әскәрmuш. Кәсир түридә берилгән тәңму-тәңликни испатлаш ­ж,әриянида өзгәрминиң қобул қилидиған мәнасини әскә елиш һаж,әт.

Мошундақ, 2- вә 3-мисалларда 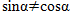  екәнлигини, 6-мисалда  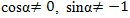әскә елиш һаж,әт.

VI. Һесап чиқириш

VІІ. Нәтижиләш. Оқуғучилар чиқарған һесаплири бойичә йәкунләймән.

VІІІ. Өйгә тапшурма.

---