Асасий тригонометриялик тәңму-тәңликләр
Алматы облысы, Ұйғыр ауданы
Долайты орта мектебінің
математика пәні мұғалімі: Даутова Махирям Телебалдыевна
9"ә" синип Алгебра
Дәрис мавзуси: Асасий тригонометриялик тәңму-тәңләр
Дәрис мәхсити: Тригонометриялик функцияләрниң хусусийәтлирини чүшәндүрүш; оқуғучиларниң есап чиқириш маһаритини ашуруш; оқуғучиларни уюшчанлиққа, коллективлиқ тәрбийләш
Дәрисниң типи: йеңи билимни өзләштүрүш
Дәрисниң усуни: чүшәндүрүш, соалға–жавап.
Пәнләр ара бағлиниши: тәбиәт, уйғур тили.
Көрнәклик қурал: таблица, карточкилар
Қолланған әдәбийәт: алгебра. 9-синип. А.Әбилқасымова, И.Бекбоев,А.Абдиева, З.Жумағулова
Дәрисниң бериши.
І. Уюштуруш.
ІІ. Өй тапшурмисини тәкшүрүш
§18. №290
ІІІ. Өткән материаллар бойича тәкрарлаш.
1. Еғизчә һесап
2. Карточка билән иш
ІV. Нәтижиләш.
Оқуғучиларниң жавави бойичә йәкүнләймән.
V. Йеңи материалға чүшүнүк.
Мәзкүр мавзуни оқуш жәриянида силәр немини үгинисиләр?
 Бу мавзуни өзләштүрүп, асасий тригонометриялик mәңму-тәңликләрниң келип чuқuш йоли билән тонушуп, бир тригонометриялик финкцияниң мәнаси бойичө қалғанлириниң мәнасини тепишқа һесаплар чиқиришни үгинисиләр.
Бу мавзуни өзләштүрүп, асасий тригонометриялик mәңму-тәңликләрниң келип чuқuш йоли билән тонушуп, бир тригонометриялик финкцияниң мәнаси бойичө қалғанлириниң мәнасини тепишқа һесаплар чиқиришни үгинисиләр.
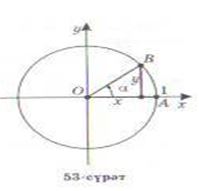
Санлиқ чәмбәрдә халиған булуңниң тригонометриялик функцияси билән тонуштуңлар вә sin α; cos α; tg α, ctg α мәналири радиусниң узунлуғиға беқинда болмайдиғанлиғини байқидиңлар. Шуниң үчүн тригонометриялик функцияни қараштурғанда радиуси 1 гә тәң чәмбәрни елиш йетәрлик. У чағда, мәсилән, силж,иғучи ОВ радиусиниң ахирқи чекитидики синус функцияси пәқәт ордината у билән, В чекитидики косинусниң мәнаси абцисса х билән ениқлинидиған болиду
(53-сүрәт).
ОВС тик булуңлуқ үчбулуңини қараштурайли. Шунда Пифагор теоремиси бойичә ОВ2 = ОС2 + ВС2, бу йәрдики ОВ = 1, ОС = х, ВС = у яки жуқурида ейтилғандәк, ОС = х = cos α; ВС = у = sin α.
Демәк, 1 = cos2 α + sin2 α
|
cos2 α + sin2 α = 1. |
(1)
Бу тәңлик α ниң халиған мәнасида дурус, йәни тәңму-тәңлик болуп hесаплиниду.
Ениқлима бойичә 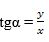 , бу йәрдики y = sinα, x = cosα болғанлиқтин
, бу йәрдики y = sinα, x = cosα болғанлиқтин
|
|
(2)
Дәл шундақ 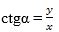 , йәни
, йәни
|
|
(3)
(1)-(3) тәңликлири бирла аргументқа бағлиқ асасий тригонометриялик тәңму-тәңликләр дәп атайду.
Булуңниң (аргументниң) һәр бир маhийити бар мәнасида һәқиқий, һәр бир функцияни ихтиярчә елинған миқдар билән алмаштурғанда һәқиқий болмайдиған тригонометриялик функцияләрдин ибарәт тәңликни тригонометриялик тәңму-тәңлик дәп атайду.
Мәсилән, (sin α + cos α)2 = sin2 α + 2 sin α ٠ cos α + cos2 α тәңму-тәңлиги тригонометриялик болмайду, сәвәви sin α вә cos α ни ихтиярчә елинған а вә b миқдарлириға алмаштурғанда, (а + b)2 = а2 + 2аb + b2 алгебрилиқ тәңму-тәңлиги чиқиду. Әнди (sin α + cos α)2 = 1 + 2 sinα ٠ cosα тәңму-тәңлиги тригонометриялик, чүнки sinα вә cosα ни ихтиярчә а вә b миқдарлириға алмаштурғанда, (а + b)2 = 1 + 2аb тәңму-тәңлик болмайду.
Әнди келәси тәңму-тәңликләрни хуласиләп чиқириш йоллирини қараштурайли.
Униң үчүн (2) вә (3) тәңму-тәңликләрни әзалап көпөйтип, мундақ тәңлик алимиз:
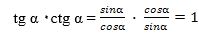
|
|
(4)
Йәни
Әгәр (1) тәңму-тәңликниң икки бөлигидә 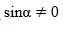 дәп елип, sin2α ға бөлсәк, у чағда
дәп елип, sin2α ға бөлсәк, у чағда
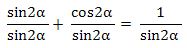
яки
|
|
(5)
Дәл мошундақ келәси тәңму-тәңликниң дуруслуғини испатлаңлар.
|
|
(6)
(1) – (6) формулилири бир аргуменmқа беқинда тригонометриялик функцияләр арисидики нисбәтләрни ипадиләйду.
1-мuсал. Әгәр 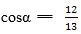 вә О < α <
вә О < α < 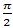 болса, у чағда sinα, tgα, ctgα ниң мәналирини тапайли.
болса, у чағда sinα, tgα, ctgα ниң мәналирини тапайли.
(1) формулидин sin2 α = 1 - соs2α чиқиду яки 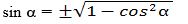
α булуңи биринчи чарәккә тәәллуқ болғанлиқтин, көрситилгән барлиқ функцияләрниң мәналири бу чарәктә — иж,абий.
Демәк,
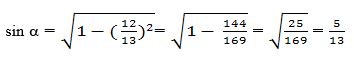
Әгәр 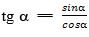 вә
вә 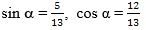 екәнлигини әскә алсақ,
екәнлигини әскә алсақ, 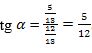 У чағда
У чағда
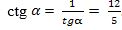
2-мuсал. Әгәр  болса, у чағда cosα, tgα вә ctgα мәналирини һесаплайли.
болса, у чағда cosα, tgα вә ctgα мәналирини һесаплайли.
Йешиш. Берилгини бойичә α булуңи ІІ чарәкниң булуңи, шуниң үчүн косинусниң тамғиси сәлбий болиду. Шунда (1) формула бойичә
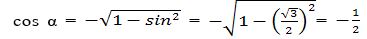
Әнди (2) вә (4) формулиларни қоллинимиз. Шунда
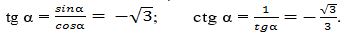
3-мисал. Әгәр 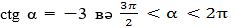 болса, у чағда sin α, cos α, tg α мәналирини тапайли.
болса, у чағда sin α, cos α, tg α мәналирини тапайли.
Йешиш. 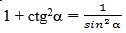 формулисидин,
формулисидин, 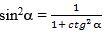 чиқиду.
чиқиду.
IV чарәктә синусниң тамғиси сәлбий болғанлиқтин,
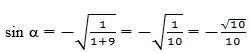 (3) формулидин
(3) формулидин
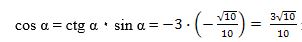 вә (4) формулидин
вә (4) формулидин
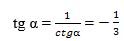 алимиз.
алимиз.
VI. Һесап чиқириш
№297
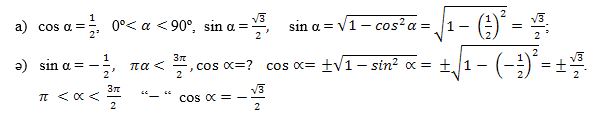
№298
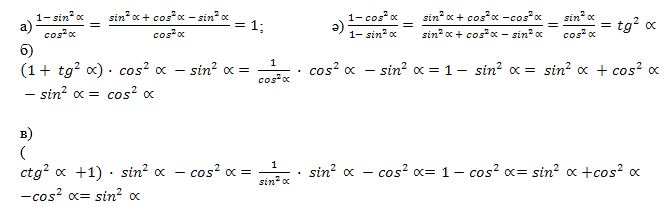
VІІ. Нәтижиләш. Оқуғучилар чиқарған һесаплири бойичә йәкунләймән.
VІІІ. Өйгә тапшурма. §19. №299
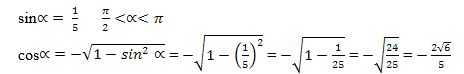
Пікірлер (1)
Пікір қалдырыңыз
Қарап көріңіз
Басқа да жазбалар
- Екі өрнектің айырмасы мен қосындысының көбейтіндісі
- 5-ке көбейту және бөлу кестесі
- Рационал сандарды салыстыру
- 5 саны мен цифры
- Алгебралық бөлшектерді қосу және азайту
- Өткенді пысықтау
- Бөлу амалының мағынасын пысықтау сабағы
- Тік төртбұрыштың (шаршының) периметрі
- Арифметикалық прогрессияның алғашқы n мүшесінің қосындысы
- Математика - қайталау сабағы
- Квадрат теңдеулер
- Тригонометриялық теңдеулерді шешу әдістері
- Масса және оның өлшем бірліктері
- Математика пәнінен ҰБТ-ға дайындық жоспары
- Масса және оның өлшем бірліктері


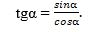
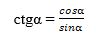
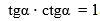
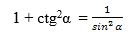
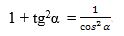

- Финли Питер Данн
- Бернард Шоу
- Виктор Франкл
- Марк Аврелий
Барлық авторлар
Ілмек бойынша іздеу
Мақал-мәтелдер
Қазақша есімдердің тізімі