Алғашқы функция. Анықталмаған интеграл

 "Қаракемер кәсіптік колледжі" МКҚК
Алгебра, геометрия пәндерінің оқытушысы: Кошмуратова Амангул Калибаевна

Сабақтың тақырыбы:  «Алғашқы функция. Анықталмаған интеграл»

Сабақтың мақсаты: Жаңа талапқа сай, жаңа ақпараттық технологияны қолдана отырып, еліміздің ертеңі болар жас ұрпаққа сапалы білім беру. Алғашқы функция және интеграл ұғымын беру және есептер шығаруда ережені қолдану.

Білімділігі: Алғашқы функцияны табуда, интегралды есептеудің тиімділігін пайдалана отырып оқушыларға тақырыптық берілген  есептерді  дұрыс, тиімді шығара білу тәсілдерін меңгерту; студенттердің алғашқы функция, интегралға арналған есептерді шешу дағдыларын жетілдіру;

Дамытушылығы: Алғашқы функцияны табу, интегралдарды есептеу кестелерін есте сақтау және оларды есептер шығаруда қолдана  білуге  дағдыландыру,  өзіндік білім көтеру қажеттілігін арттыру;

Тәрбиелігі: Коммуникативті құзіреттілігін қалыптастыру; өз күшіне сену жеке тұлғалық қарым-қатынастық қабілеттерін қалыптастыру.

Оқыту әдiстерi: практикалық, iзденiс, проблемалық, зерттеушiлiк.

Сабақтың түрі: Зерттеушілік типті теориялық және практикалық сабақ.

Пән аралық байланыс: физика, информатика

Көрнекіліктер: Интерактивті тақта.

Сабақтың барысы:

Сабақтың мақсатымен таныстыру.

І. Мотивациялық-танымдық кезең.

(Оқушылардың ойлау іс-әрекетін белсенділікке бағыттау)

Туынды ұғымы деген не? Туындының геометриялық және физикалық мағынасы? Туындының анықтамасы қалай беріледі? Туындыны табудың ережелері.

Қарапайым функциялардың  туындыларының кестесі

ІІ.Өткенді пысықтау.

1. (с)`=

 2. (х)`=  

3. (1/х)`=

4. (√x)`=

5. (хⁿ)`=

6. (sinx)`=

7. (cosx)`=

8. (tgx)`=

9. (ctgx)`=

10. (u+v)`=

11. (u·v)`=

12. (u/v)`=

13. f(g(x))`=  

ІІІ. Жаңа сабақ.

 Механикада материалдық нүктенің жүрілген жолы белгілі болғандаоның жылдамдығын, үдеудін туындыны қолданып табуға болады. S`(t)=v(t); a(t)=v`(t) болады.

Алайда механикада матералдық нүктенің үдеуі a(t); жылдамдығы v(t) белгілі болғанда s(t)-ті жолды есептеуге тура келеді. Мұндай есептерді шығару үшін дифференциялдау амалына кері амалы интегралдау қолданады.

Интегралдау – берілген барлық функцияларын табу.

Егер f ^'(x) = 2x  болса, онда f (x)  функциясы қалай өрнектеледі? Ол функция f (x) = x² болып табылады. Оның дұрыстығын қалай тексеруге болады?

Алғашқы функция анықтамасы, белгіленуі беріледі.

Келесі мысалдарды орындап, салыстыру жасай отырып ереже қорытып беріңіз.

Мысалдар қарастыру.  f (x) = 5 болса,   ондаF(x) =   ;

f (x) = 25 болса, онда  F(x) =   ;   f (x) = π болса, онда  F(x) =   ; 

Қандай қорытынды жасауға болады?  (Тұрақты санның алғашқы функциясы)   

Енді  f (x) = 5х⁴ функциясы үшін келесі функциялардың қайсысы алғашқы функциясы болады?  F(x) = х⁵+9  , F(x) = х⁵−64  , F(x) = х⁵+100 , F(x) = х⁵−164

Қандай қорытынды жасауға болады? 

Зерттеу жасай келе, бұл функциялардың барлығы да берілген функция үшін алғашқы функция болатынын көруге болады. Демек f (x) үшін алғашқы функциясы жалпы түрі

 F(x) + С болады, С – тұрақты сан.

Алғашқы функцияның негізгі қасиеті ұғымы беріледі.

Жоғарыда қарастырылған мысалдағы алғашқы функциялардың графиктері туралы не айтуға болады? (Олар параллель орналасады)

Алғашқы функцияны табудың  үш ережесін беру.

1) Егер F(x) функциясы  f(x) функциясының, ал Р(х) функциясы р(х) функциясының алғашқы функциялары болса, онда F(x)+ Р(x) функциясы f(x)+ р(х) функциясының алғашқы функциясы болады.

2) Егер F(x) функциясы f(x) функциясының алғашқы функциясы,ал k-тұрақты болса, онда k F(x) функциясы kf(x)функциясы үшін алғашқы функция болады.

3) Егер F(x) функциясы f(x) функциясының алғашқы Функциясы, ал k және b - тұрақтылар болса, онда функциясы

f (kx+b)  = 1/k*F(kx+b) функциясы үшін алғашқы функция болады.

Интерактивті тақтаның көмегімен қарапайым интегралдар кестесі беріледі.

IV. Кім жүйрік?

1. f(x)=3x+2                               F(x)=?
2. f(x)=cos²x-sin²x                      F(x)=?
3. f(x)=3x²                                 F(x)=?
4. f(x)=9x⁸                                 F(x)=?
5. f (x)=18x¹⁷                             F(x)=?
6. f(x)=5x⁴                                 F(x)=?
7. f(x)=2cosx                             F(x)=?
8. f(x) = 3x² −2                          F(x)=?

V. Жаңа сабақты бекіту.

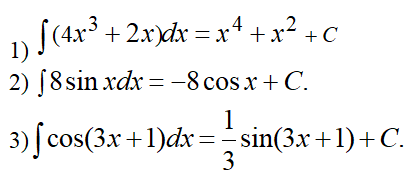
Есептер шығару

Оқулықтағы деңгейлік тапсырмалар бойынша өз бетімен, жұпта, топпен жұмыс. Оқушы өз деңгейіне қарай тапсырмалар бойынша жұмыс жасайды. А.Е. Әбілқасымова оқулығы бойынша:

А деңгейі: №1 (ауызша),  №3,  №6(2,4), №7

В деңгейі: №8(2,4), №9(2,4), №11

Есептердің шешyі:    

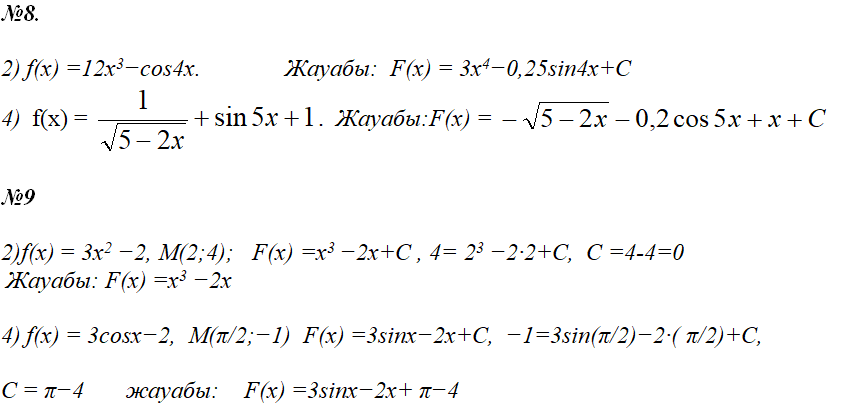
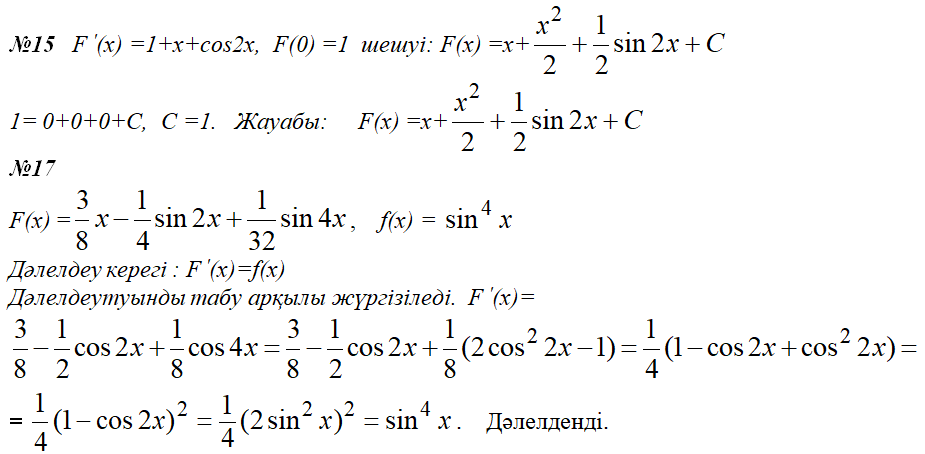
 VI. Үйге тапсырма: Тақырыптағы ережелерді, формулаларды оқып келу

№8-9 есеп

VII. Қорытындылау

Сөйлемдерді аяқтаңыз:

1)  F ^'(x)=f(x)  теңдігі орындалса, онда  ................................................................

2)  f(x) үшін алғашқы функцияның жалпы түрі  ..................................................

3) Алғашқы функцияның геометриялық мағынасы ол,   .......................................

4) 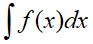 белгісі  .......................................................................................

5)  f(x) + p(x) үшін алғашқы функция  ..................................................................

6) k f(x) үшін алғашқы функция  .........................................................................

7) f (kx+в) үшін алғашқы функция   ....................................................................

Үй тапсырмасы. Әбілқасымова А.Е.№2, №4 №8(1,3), №9(3,4) В деңгейі

VIІI. Бағалау кезеңі.  Сабаққа жақсы қатысып өз білімін көрсетіп, сұрақтарға жауап беріп белсенді қатысып отырған білім алушыларды бағалау.

 IX. Рефлексивті кезең. Еркін микрофон

1. Бүгінгі сабақта нені үйрендік?
2. Есептер сіздер үшін күрделі болды деп ойлайсызба?
3. Қай есеп күрделі болды? Неге?

---