Математикалық және серіппелі маятниктердің тербелістері

"Қаракемер кәсіптік колледжі" МКҚК
Физика пәнінің оқытушысы: Дүйсенбек Камила

Сабақтың тақырыбы: Математикалық және серіппелі маятниктердің тербелістері

Сабақтың мақсаты:

Білімділік:  Табиғаттағы ең көп тараған қозғалыс бірдей уақыт аралықтарында дәлме-дәл немесе шамамен қайталанып отыратын тербелісін сипаттайтын шамаларды қайталау арқылы жаңа тербелмелі жүйелермен танысу. Маятниктің тұрмыстағы техникадағы, өмірдегі және эволюциялық прцестегі рөлін анықтау.

Дамытушылық: Оқушылардың бірін-бірі тыңдай білу, өз ойын тиянақты жеткізе білу, нақты сұрақ қойып, қойылған сұраққа дәл жауап бере білу қабілеттерін дамыту. Алған білімін спалық сипаттағы есептер мен жауаптар іздестіруге қолдана білу.

Тәрбиелік: Оқушылардың танымдық қызығушылығын арттыра отырып, тербелістердің қасиеттері мен өмірде алатын орнын зерттеп білу қажеттілігін өздігінен түсініп, білімді өз күшімен алуға ұмтылысын тәрбиелеу.

Сабақтың түрі: Жаңа сабақ.

Сабақтың дидактикалық қамтамасыз етілуі: карточкалар, электронды оқулық, интерактивті тақта

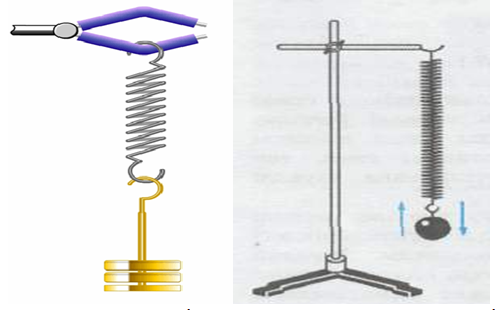
Құрал жабдықтар: Штатив, жіп, серіппе, денелер, сағат, сызғыш.

Сабақтың барысы

І Ұйымдастыру кезеңі.

- Сәлеметсіңдер ме, балалар? /түгендеу/.

Оқушылардың ыңғайларына қарап, ұйымдастыру.

ІІ Үй тапсырмасын тексеру.

Үй тапсырмасын орындауларын тест арқылы тексеру.

ІІІ Жаңа сабаққа дайындық

/Математикалық және серіппелі маятниктердің қозғалыс динамикасын көрсетіп, оқушылармен бірге талдап, ситуациялық проблемалар қойып, жаңа тақырыпқа көшу./

-    Балалар сендердің алдарыңда екі түрлі тербелмелі жүйе бар. Екеуінде қандай айырмашылықтар көріп тұрсыңдар?
-    Олардың айырмашылықтары: тербеліс периодтарының әр түрлі екендігінде.

Маятниктердің түрлерімен таныстырып, олардың периодын, жиілігін анықтауды үйрету.

ІV Жаңа сабақ

Тербелмелі процестер жүзеге асатын құрылғыларды тербелмелі жүйелер деп атайды. Осындай жүйелердің қарапайым түрі - математикалық және серіппелі маятник.

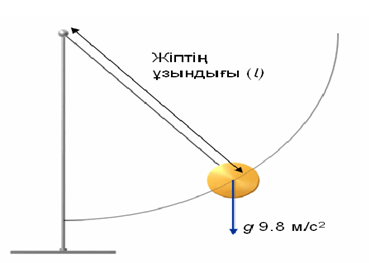
Математикалық маятник деп созылмайтын салмақсыз жіңішке ұзын жіпке  ілінген кішкентай ауыр шарды айтады.

Егер маятниктің ұзындығын өзгертпей, оған массалары әр түрлі жүктер ілсек, онда маятниктің тербеліс периодының өзгермейтіндігі байқалды.

Математикалық маятниктің периоды жүктің массасына тәуелді болмайды.

2.  Егер маятникті қозғалысқа келтіргенде оны әр түрлі бұрьшқа (бірақ өте үлкен емес) ауытқытатын болсақ, онда ол амплитудасы түрліше болғанымен, бірдей периодпен тербелді.

Математикалық маятниктің периоды тербеліс амплитудасына тәуелді болмайды.

Маятник неғұрлым ұзын болса, тербеліс периоды соғұрлым көп болды. Ал, керісінше, маятник неғұрлым қысқа болса, тербеліс периоды соғұрлым аз болды.

Тербеліс периоды маятник ұзындығына тәуелді болады.

Маятниктің тербеліс периодының еркін түсу үдеуіне тәуелді болатын-дығы тәжірибеде жер бетінің әр түрлі нүктелеріндегі еркін түсу үдеуін дәл өлшеу үшін пайдаланылады. Мұндай құралдардың негізгі тетігі маят-ник болғандықтан, оларды маятникті құралдар деп атайды. Жер бетінің қажет аймағындағы еркін түсу үдеуін өлшеу үшін сол жерге маятникті құралдарды орнатады да, маятниктің Т тербеліс периодын өлшейді. Периодтың алынған мәні мен маятниктің белгілі  ұзындығы бойынша сол жердегі еркін түсу үдеуі есептеледі. Еркін түсу үдеуін есептеу нәтижелері бойынша пайдалы қазба байлықтар қоры жатқан аймақты анықтауға болады.

Жіпке немесе серіппеге ілінген жүктің тер-беліс периодының тербеліс амплитудасына тәуелді болмайтындығын 1583 ж. итальяндық ұлы физик әрі астроном Галилео Галилей ашқан болатын. Бұл жаңалық де-нелердің механикалық тербелістерінің алғашқы негізгі заңдарының бірі болып табы-лады. Аңыз бойынша Галилей бұл жаңалықты шіркеудегі шырақтың шайқалуын бақылай отырып ашқан екен.  Галилей ма-ятниктің тербеліс периодының оның амплитудасына тәуелді болмайтынын тәжірибе жүзінде дәлелдей отырып, маятниктерді уақыт өлшеуіші ретінде сағат- тарда пайдалануды ұсынды. Алайда тек 70 жылдан астам уақыт өткенде, 1656 ж. X. Гюйгенс осы идеяны жүзеге асырып, алғаш рет маятникті сағат құрастырып шығарды.

Математикалық маятник тербеліс периодының формуласын қорытып шығарайық .

 

Маятник тербеліп тұрғанда жүк АВ доғасының бойымен Ғ_қ кері қайтарушы, яғни қорытқы күштің әрекетінен үдеумен қозғалады. Бұл күштің шамасы қозғалыс кезінде өзгеріп отырады. Дененің тұрақсыз күштің әрекетінен қозғалысын есептеу өте күрделі.

         

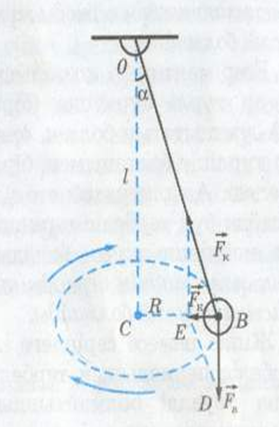
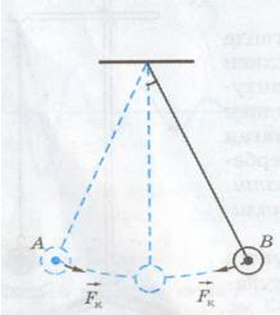
Сондықтан есепті жеңілдету үшін маятникті бір жазықтықта тербелтпей, жүк шеңбер бойымен қозғалатындай етіп, оны конус сызуға мәжбүр етеміз.

Маятниктің айналу периоды оның тербеліс периодына тең болады. Т_айн.=Т_тер=Т.

Конустық маятниктің айналу периоды жүк сызатын шеңбердің ұзындығын сызықтық жылдамдыққа бөлгенге тең:

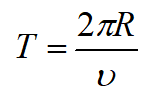
Ал маятник вертикаль күйінен шамалы ғана ауытқитын болса, амплитуда аз болғанда, қорытқы күш шеңбердің ВС радиусы бойымен бағытталады деп есептеуге болады. Бұл жағдайда қорытқы күш центрге тартқыш күшке тең:                 

      

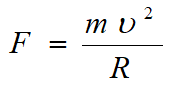
ОВС және ВDE үшбұрыштарының ұқсастығынан:

ВЕ:ВD = СВ:ОС немесе Ғ:mg = R:l, бұдан          

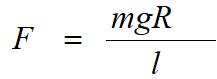
Ғ күшінің осы екі өрнегін теңестіре отырып алатынымыз:     

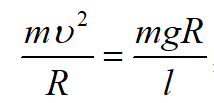немесе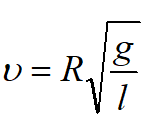  

Осыны Т периодтың өрнегіне қойып, мынаны аламыз:

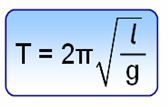
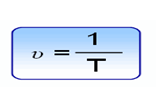
болғандықтан, математикалық маятниктің жиілігін мына өрнек арқылы шығара аламыз:

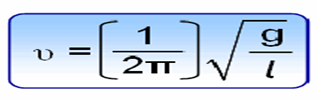
Математикалық маятниктің жібінің ұзындығы мына өрнек арқылы есептеледі:

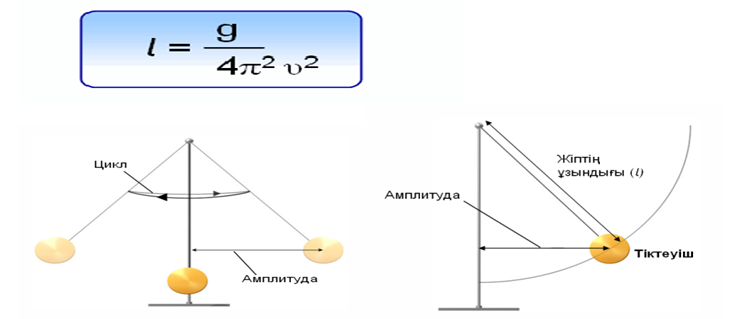
Енді серіппеге ілінген жүктің тербелісін қарастырайық.

Мұндай қарапайым тербелмелі жүйені серіппелі маятник деп атайды.

Егер серіппе l ұзындыққа созылса немесе сығылса, онда денені тепе-теңдік күйіне қайтаратын Ғ күші туындайды. Ұзару шамасы азғантай болған кезде бұл күш серіппенің ұзаруына пропорционал болады, яғни Гук заңы бойынша: Ғ= -k*x

Ньютонның 2-ші заңын пайдалансақ, дененің қозғалыс теңдеуін мына түрде жазуға болады: 

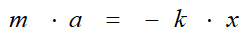бұдан,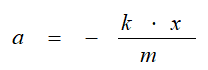 

Гармоникалық тербелістердің жиілігі 1с ішіндегі тербелістер санын көрсетсе, циклдік жиілік секундтағы тербелістер санына тең болады, яғни: 

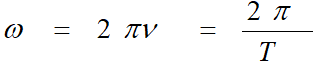
Олай болса, 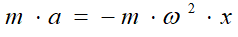. Осы өрнекті қозғалыс теңдеуімен салыстыра отырып алатынымыз:

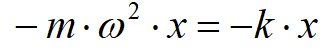
Бұдан 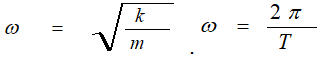   екенін ескерсек, серіппелі маятниктің

периоды мынаған тең болады:

 

Серіппелі маятниктің тербеліс периоды тек жүк массасы мен серіппенің қатаңдығына тәуелді болады.

Серіппелі маятниктің жиілігін мына өрнек арқылы шығара аламыз:

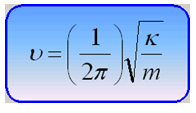
Серіппелі маятниктің қатаңдық коэффициенті мына формуламен анықталады:

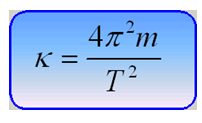
Серіппелі маятникке ілінген жүктің массасы мына өрнек арқылы есептеледі:

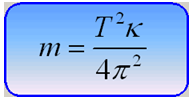
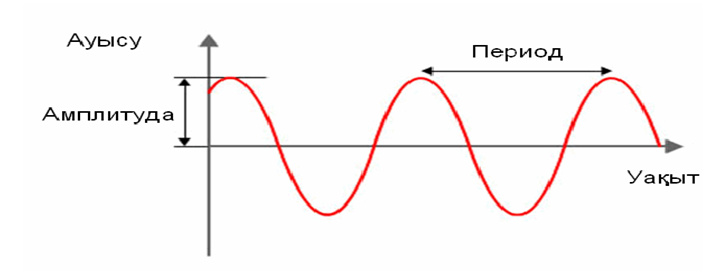
Маятник тербелісінің графигі синусойда немесе косинусойда түрінде болады.

V. Сабақты бекіту:

1. Математикалық маятник деп нені айтады?
2. Серпімділік күші әрекет еткен дененің тербеліс периоды неге тәуелді болады?
3. Маятник қай жерлерде пайдаланылады?

1. Қатаңдығы 9,22 Н/м серіппеге ілінген массасы 0,143 кг жүктің тербеліс периодын және жиілігін анықтаңдар.
2. Қатаңдығы 250 Н/м серіппеге 16 с ішінде 20 тербеліс жасйтын жүктің масасын табыңдар.
3. Қатаңдығы 12,3 Н/м серіппеге ілінген массасы 0,211 кг жүктің тербеліс периодын және жиілігін анықтаңдар.

VI.Үйге тапсырма:

1. §27 оқып келу.
2. жаттығу №22 3, 4есеп
3. А.П.Рымкевич №409, 410, 415, 419

VII.Бағалау: Өзіңді - өзің тексер! Карточкамен жұмыс

---