Дурус көпбулуңлуқлар. Топмақ көпбулуңлуқлар
Алматы облысы, Ұйғыр ауданы
"Долайты орта мектебі" КММ-сінің
математика және физика пәні мұғалімі
Даутова Махирям Телебалдыевна
9 "а" Геометрия
Дәрис мавзуси: Дурус көпбулуңлуқлар. Топмақ көпбулуңлуқлар.
Дәрис мәхсити:
1) Оқуғучиларға көпбулуңлуқларни чүшәндүрүш;
2) Оқуғучиларниң есап чиқириш маһаритини ашуруш;
3) Оқуғучиларни әмгәк тәрбийәсигә тәрбийләш.
Дәрисниң типи: Йеңи билимни өзләштүрүш.
Дәрисниң усуни: чүшәндүрүш, соалға–жавап.
Пәнләр ара бағлиниши: тәбиәт, уйғур тили.
Көрнәклик қурал: сизғуч, фигурлар, карточкилар.
Қолланған әдәбийәт: геометрия. 9-синип. С.Шәкиликова, Ж.Нурпейис, Ғ.Қалдыбаева
Дәрисниң бериши.
І. Уюштуруш.
ІІ. Өй тапшурмисини тәкшүрүш №285
ІІІ. Өткән материаллар бойича тәкрарлаш.
1. Еғизчә һесап
2. Карточка билән иш
ІV. Нәтижиләш.
Оқуғучиларниң жавави бойичә йәкүнләймән.
V. Йеңи материалға чүшүнүк.
Дурус көпбулуңлуқлар. Топмақ көпбулуңлуқлар.
Алдинқи синиплардин бизгә дурус үчбулуңлуқ (тәң тәрәплик үчбулуңлуқ) вә дурус төртбулуңлуқ (квадрат) бәлгүлүк. Әнди көпбулуңлуқлар чушәнчисини берип, дурус көпбулуңлуқларға тохтилимиз.
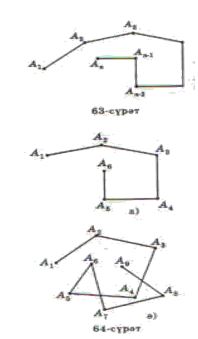 А1, А2,..., Аn чекитлиридин вә мошу чекитләрни қошидиған А1А2, А2Аз,..., Аn-1Аn кесиндилиридин ибарәт фигурини сунуқ сизиқ дәп атаймиз (63-сурәт).
А1, А2,..., Аn чекитлиридин вә мошу чекитләрни қошидиған А1А2, А2Аз,..., Аn-1Аn кесиндилиридин ибарәт фигурини сунуқ сизиқ дәп атаймиз (63-сурәт).
А1, А2, ... , Ап чекитлиридин А1А2...Аn сунуқ сuзuгuнuң чоққuлuрu дәп, А1А2, А2Аз,..., Аn-1Аn кесиндилирини болса сунуқ сизиқниң звенолири дәп атайду.
Әгәр сунуқ сизиқниң звенолири өз ара қийилишмиса, у чағда мундақ сизик аддий сизиқ дәп атилиду.
63, 64, а-сүрәтләрдә аддий сунуқ сизик,
64, ә-сүрәттә мүрәккәп сунуқ сизиқ көрситилгән.
А1А2... Ап сунуқ сизиғиниң дәсләпки А1 чекити шу cyнyқнuң башлиниши дәп, ахирқи Ап чекити сунуқнuң учu дәп атилиду.
Әгәр сунуқ сизиқниң башлиниши вә учи дәлму-дәл кәлсә, у чағда мундақ сунуқ туюқ сунуқ (туюқ сунуқ сизиқ) дәп атайду.
Туюқ аддий сунуқ сизиқ көnбулуңлуқ дәп атилиду. Сунуқ сизиқниң чоққилири көnбулуңлуқнuң чоққилири, сунуқ сизиқниң звенолири көпбулуңлуқниң тәрәплири дәп атилиду. Көпбулуңлуқни униң чоққилириниң сани, демәк, тәрәплириниң сани бойичә атайду.
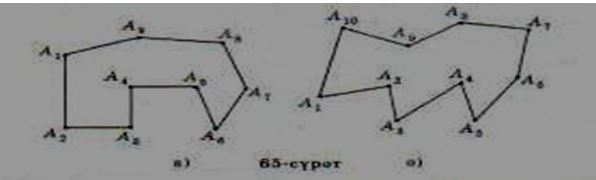
65, ә-сүрәттә А1А2...А10 көпбулуңлуғида А1, A2,..., АІ0 - униң чоққилири, АІА2, А2Аз, ... , А10А1- онбулуңлуқниң тәрәплири. Көпбулуңлуқниң хошна әмәс икки чоққисини туташтуридиған кесиндә көnбулуңлуқнuң диагонали дәп атилиду,
мәсилән, 66-сүрәттә A1 A2A4A5 бәш булуңлуғида А1А3, А1А4, A2A4, A2A5, А3А5 кесиндилири - бәшбулуңлуқниң диагональлири.
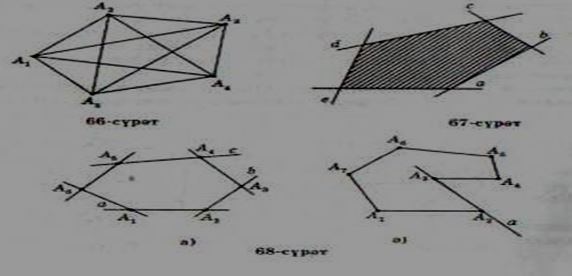
Әгәр көпбулуңлуқ униң тәрәплирини өз ичигә алған һәр бир түзгә нисбәтән бир йерим тәкшиликтә ятса, у чағда мундақ көпбулуңлуқ томпақ көnбулуңлуқ дәп атилиду (67 -сүрәт), 67 вә 68, а -сүрәттә томпақ көпбулуңлуқ, 68,ә – сүрәттә томпақ әмәс көпбулуңлуқ көрситилгән.
Томпак көпбулуңлуқниң ениқлимисидин һәр қандақ үчбулунлуқ томпақ көпбулуңлуқ екәнлиги чиқиду, бирақ төртбулуңлуқ үчүн бу хусусийәт орунланмайду,
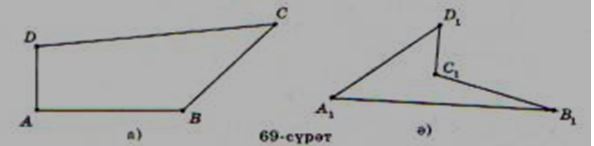
мәсилән, 69, а-сүрөт томпақ, 69, ә-сүрәттә томпақ әмәс көпбулуңлуқ тәсвирләнгән.
1 9 - т е о р е м а. Томпақ п – булуңлуқ көпбулуңлуқниң ички булуңлириниң қошиндиси 180º(п – 2) гә тәң.
И с п а т л а ш. Чоққилири А1, А2, ..., Ап болидиған көпбулуңлуқ берилгән (70-сүрәт). Көпбулуңлуқниң ичидин һәр қандақ бир О чөкитини елип, О чөкитини көпбулуңлуқниң А1, А2,..., Ап чоққилири билән қошуп, үчбулуңлуқлар алимиз (көпбулуңлуқниң тәрәплириниң сани n вә бу тәрәпләр қараштурулуватқан үчбулуңлуқларниң асаслири; үчбулуңлуқлар О чекитидә қошулиду). Бу кесиндиләр көпбулуңлуқни чоққиси О чекити болидиған, асаслири көпбулуңлуқнин тәрәплири болидиган п үчбулуңлуққа бөлиду. Мошу п үчбулуңлуқниң барлиқ ички булуңлириниң қошундиси 180ºn. Көпбулуңлуқниң ички булуңлириниң қошундисини тепиш үчүн бу қошундидин (180ºn кошундисидин) 360º-ни, йәни О чоққисидики барлиқ үчбулуңлуқларниң чоққилириниң булуңлириниң қошундисини кемитимиз, ундақ болса көпбулуңлуқниң ички булунлириниң қошундиси төвәндикигә тәң:
180ºn - 360º = 180º (n -- 2). Теорема испатланди.
Әгәр томпақ көпбулуңлукниң барлиқ булуңлири вә барлиқ тәрәплири өз ара тәң болса, у чағда мундақ томпақ көпбулуңлуқ дурус көnбулуңлуқ дәп атилиду, 71-сүрәттә томпақ дурус бәшбулуңлуқ тәсвирләнгән.
Әгәр көпбулуңлуқниң барлиқ чоққилири қандақту бир чәмбәрниң бойида ятса, у чағда көпбулуңлуқ чәмбәр ичидин сизилған яки чәмбәр көпбулуңлуққа тешидин сизилған дәйду (72, а-сүрәт). Әгәр көпбулуңлуқниң барлиқ тәрәплири қандақту бир чәмбәргә яндашса, у чағда көn6улуңлуқ чәмбәргә тешидин сизилған яки чәмбәр көnбулуңлуққа ичидин сизилган дөйду (72, ә-сүрәт),
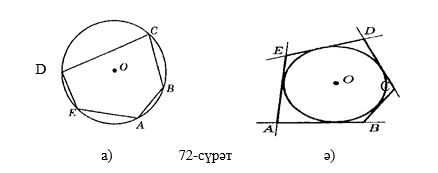
20 - т е о р е м а . Дурус көnбулуңлуқ қандақту бир чәмбәргә ичидин сизилган яки чәмбәргә тешидин сизилган болуn hесаnлuнuду.
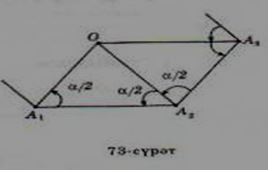
Ис п а т л а ш . А1 вә А2 чекитлири дурус көпбулуңлуқниң хошна икки чоққиси болсун (73-сүрәт). Дурус көпбулуңлуқ болғанлиқтин,
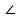 А1=
А1=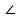 А2 = α. Әнди А1, А2 чоққилиридики булуңларниң биссектрисилирини жүргүзсәк, О чекитидә қийилишиду. А1ОА2 үчбулуңлуғи тәң янлиқ, сәвәви ОА1, ОА2 кесиндилири өз ара тәң А1 вә А2 булуңлириниң биссектрисилири:
А2 = α. Әнди А1, А2 чоққилиридики булуңларниң биссектрисилирини жүргүзсәк, О чекитидә қийилишиду. А1ОА2 үчбулуңлуғи тәң янлиқ, сәвәви ОА1, ОА2 кесиндилири өз ара тәң А1 вә А2 булуңлириниң биссектрисилири:
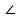 ОА1А2= α/2,
ОА1А2= α/2, 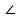 ОА1А2 =
ОА1А2 = 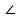 ОА2А1. Буниңдин ОА1 = ОА2. Әгәр О чекитини көпбулуңниң кейинки А3 чоққиси билән қошсақ, өз ара тәң ОА1А2 вә ОА2А3 үчбулуңлуқлирини алимиз:
ОА2А1. Буниңдин ОА1 = ОА2. Әгәр О чекитини көпбулуңниң кейинки А3 чоққиси билән қошсақ, өз ара тәң ОА1А2 вә ОА2А3 үчбулуңлуқлирини алимиз:
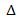 ОА1А2 =
ОА1А2 = 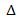 ОА2А3 (ОА2 – умумий тәрәп, А1А2 = А2А3,
ОА2А3 (ОА2 – умумий тәрәп, А1А2 = А2А3, 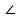 ОА2А3 =
ОА2А3 = 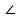 ОА2А1; үчбулуңлуқлар тәңлигиниң биринчи бәлгүси). Үчбулуңлуқлар тәңлигидин
ОА2А1; үчбулуңлуқлар тәңлигиниң биринчи бәлгүси). Үчбулуңлуқлар тәңлигидин 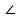 ОА3А2 = α/2. Ундақ болса, А3 чоққисидики булуңиму α болғанлиқтин, ОА3 кесиндиси – А3 чоққисиниң биссектрисиси. ОА2А3 үчбулуңлуғи тәң янлиқ болса ОА3 = ОА2.
ОА3А2 = α/2. Ундақ болса, А3 чоққисидики булуңиму α болғанлиқтин, ОА3 кесиндиси – А3 чоққисиниң биссектрисиси. ОА2А3 үчбулуңлуғи тәң янлиқ болса ОА3 = ОА2.
Шундақ қилип, О чекити көпбулуңлуқниң А1, А2, А3 чокқилиридин бирдәк жирақлиқта орунлашқан: ОА1=ОА2=ОА3 болиду. О чекити дурус көпбулуңлуқниң қалған чоққилиридинму бирдәк арилиқта орунлашқини мошу усул билән испатлиниду. Бу ейтилғанлардин төвәндики хуласигә келимиз: О чекити – дурус көпбулуңлуққа тешидин сизилған чәмбәрниң мәркизи.
 Шуниң билән биллә О чекити А1, А2, Аз, ... чоққилиридин жүргүзүлгән биссектрисиларниң қийилишиш чекити болғанлиқтин (үчбулуңлуққа ичидин сизилған чәмбәрниң хусусийити яки биссектриса дегинимиз - булуңниң тәрәплиридин бирдәк арилиқта орунлашқан чекитләрниң жиғиндиси), көпбулуңлуқниң барлиқ тәрәплири мәркизи О чекитидә, радиуси болса О чекитидин жүргүзүлгән үчбулуңлуқларниң егизликлиригә тәң болидиған чәмбәрни яндишидиғанлиғи чиқиду. Теорема испатланди.
Шуниң билән биллә О чекити А1, А2, Аз, ... чоққилиридин жүргүзүлгән биссектрисиларниң қийилишиш чекити болғанлиқтин (үчбулуңлуққа ичидин сизилған чәмбәрниң хусусийити яки биссектриса дегинимиз - булуңниң тәрәплиридин бирдәк арилиқта орунлашқан чекитләрниң жиғиндиси), көпбулуңлуқниң барлиқ тәрәплири мәркизи О чекитидә, радиуси болса О чекитидин жүргүзүлгән үчбулуңлуқларниң егизликлиригә тәң болидиған чәмбәрни яндишидиғанлиғи чиқиду. Теорема испатланди.
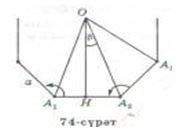
М ә с и лә. Тәрипи а болидиған дурус n-булуңлуққа тешидин вә ичидин сизилған чәмбәрләрниң R вә r радиуслирини тепиш керәк.
Й е ш и ш. Дурус n-булуңлуқниң чоққисидики булуңи α болсун (74-сүрәт), шунда
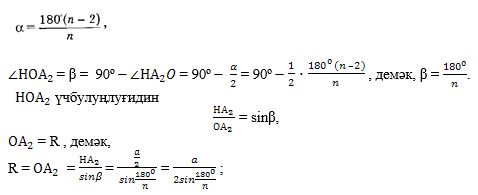
Тәң янлиқ А1ОА2 үчбулуңлуғиниң ОН егизлиги көпбулуңлуққа ичидин сизилған чәмбәрниң радиуси болғанлиқтин,
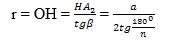
Айрим һаләтләрдә: 1) дурус үчбулуңлуқ (тәң тәрәплик үчбулуңлуқ) үчүн: n = 3, α = 180º:3 = 60º
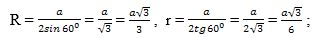
2) дурус төртбулуңлуқ (квадрат) үчүн: n = 4; α = 180º:4 = 45º.
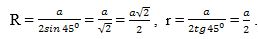
VI. Һесап чиқириш
№296
б) һәр қандақ томпақ көпбулуңлуқ дурус көпбулуңлуқ болиду
№297
5, 6, 8, n – булуңлуқ көпбулуңлуқниң һәр бир чоққисидин қанчә диоганаль жүгүзүшкә болиду?
5 – 2диоганаль, 6 – 3диоганаль, 8 – 5диоганаль
VІІ. Нәтижиләш. Оқуғучилар чиқарған һесаплири бойичә йәкунләймән.
VІІІ. Өйгә тапшурма. §21. № 299.
Пікірлер (1)
Пікір қалдырыңыз
Қарап көріңіз
Басқа да жазбалар
- Екі өрнектің айырмасы мен қосындысының көбейтіндісі
- 5-ке көбейту және бөлу кестесі
- Рационал сандарды салыстыру
- 5 саны мен цифры
- Алгебралық бөлшектерді қосу және азайту
- Өткенді пысықтау
- Бөлу амалының мағынасын пысықтау сабағы
- Тік төртбұрыштың (шаршының) периметрі
- Арифметикалық прогрессияның алғашқы n мүшесінің қосындысы
- Математика - қайталау сабағы
- Квадрат теңдеулер
- Тригонометриялық теңдеулерді шешу әдістері
- Масса және оның өлшем бірліктері
- Математика пәнінен ҰБТ-ға дайындық жоспары
- Масса және оның өлшем бірліктері



- Финли Питер Данн
- Бернард Шоу
- Виктор Франкл
- Марк Аврелий
Барлық авторлар
Ілмек бойынша іздеу
Мақал-мәтелдер
Қазақша есімдердің тізімі