Арифметическая и геометрическая прогрессии в заданиях ВОУД

Учитель математики Амиржанова Рауза Жаслыковна
Шалдайская СОШ
С. Шалдай

Цели урока:

— Обобщить и систематизировать знания учащихся по данной теме.
— Разобрать типичные задания встречающихся в сборниках для подготовки к ВОУД.
— Проверить степень усвоения материала.

Ход урока:

1. Организационный момент.

2. Повторение. (опрос- тест) (слайды 3-13 )

Арифметическая прогрессия – это последовательность….

1	2	3
каждый член которой, начиная со второго, равен предыдущему члену умноженному на одно и то же число.	Каждый член которой, начиная со второго, равен предыдущему члену сложенному с одним и тем же числом.	Каждый член которой, равен предыдущему члену сложенному с одним и тем же числом.

 

Геометрическая прогрессия – это последовательность….

1	2	3
Отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену  умноженному на  одно и то же число.	каждый член которой, равен предыдущему члену  умноженному на  одно и то же число.	каждый член которой, начиная со второго, равен предыдущему члену умноженному на  одно и то же число.

 

Формула для нахождения разности арифметической прогрессии

1	2	3

 

Формула для нахождения знаменателя геометрической прогрессии.  

1	2	3
	q=an+1/an	q=an/an+1

 

Формула  n–ого члена арифметической  прогрессии

1	2	3

 

Формула  n – ого члена геометрической прогрессии

1	2	3

 

Формула суммы n – первых членов арифметической прогрессии.

1	2	3

 

Формула суммы n – первых членов геометрической прогрессии.

1	2	3

 

Последовательности заданы несколькими первыми членами . Одна из них геометрическая прогрессия. Найдите ее.

1	2	3	4

 

Арифметическая прогрессия (b_n) задана условием: b₁=4, b_n+1=b_n+5 Найдите b₂

1	2	3	4
5	45	9	6

 

Записано несколько последовательных членов геометрической прогрессии. Найдите член прогрессии обозначенной х

1	2	3	4
7		1	2

 

Члены последовательности можно изображать точками на координатной плоскости. Для этого по горизонтальной оси откладывают номер члена, а по вертикальной – соответствующий член последовательности.

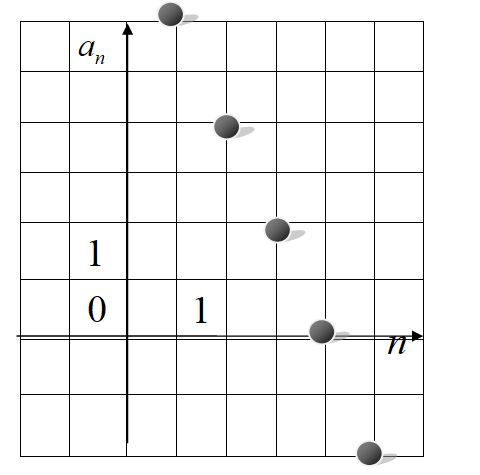
На рисунке изображены точками первые пять членов арифметической прогрессии. Найдите первый член прогрессии и разность прогрессии.

3. Систематизация знаний

Задача №1

Последовательность арифметическая прогрессия. Найдите сумму первых четырех ее членов, если а₁=8, а₃=18.

Задача №2

Арифметическая прогрессия а_{n -}  задана несколькими членами:  Найдите ее 2012 член.

Задача №3

a_n  - арифметическая прогрессия. a₄=3   a₉=-17. Найдите разность этой прогрессии.

Задача №4

В арифметической прогрессии  , а сумма первых семи членов равна 28. Найдите первый член и разность прогрессии.

Задача №5

Сколько надо сложить последовательных натуральных чисел, кратных 7, что бы их сумма была равна 546

Задача №6

С_n – геометрическая прогрессия, знаменатель прогрессии равен -5, первый член -5. Найдите сумму первых четырех ее членов.

Задача № 7

С_n геометрическая прогрессия,а₃=-3,а₈=-96. Найдите знаменатель этой прогрессии.

Задача № 8

Дана геометрическая прогрессия.    Найдите произведение первых пяти ее членов.        

Задача № 9

Найдите сумму первых шести членов геометрической прогрессии (а_n ), если известно, что  и S₃=42.

Задача № 10

В геометрической прогрессии разность между шестым и четвертыми членами равна 192, а разность между третьим и первым членами равна 24. Найдите сумму первых восьми членов этой прогрессии.                                                                                                                                                                                 

4. Самостоятельная работа ( тест)

Вариант-1	Вариант -2
1.Найдите семнадцатый член арифметической прогрессии: -4; -2; 0; ... 1) -28            2)   29           3) 30           4) 28	1.Найдите сумму первых двенадцати членов арифметической прогрессии: 26; 10;... 1)265         2) -477        3) 567           4)-744
2.Найдите сумму первых пяти членов геометрической прогрессии, если ее первый член равен 8, а знаменатель прогрессии равен 0,5 1) 15         2) 15,5        3)11             4)-15,5	2.Записано несколько последовательных членов арифметической прогрессии. Найдите член прогрессии обозначенной х  5; 8; х; 14;… 1)  3           2)-11        3)  11         4)10
3. Какая из данных последовательностей является геометрической прогрессией? 1)	3.Найдите шестой член геометрической прогрессии если известно, что первый член равен 3, а знаменатель 2. 1) 96,5         2) 96          3) 69            4)-96
4.Между числами 3 и 18 вставьте четыре числа, которые вместе с данными образуют арифметическую прогрессию.   1)  6; 9; 12; 15             2)-6;-9;-12;-15                  3)  6; -9; 12; -15           4)-6: 9 -12; 15	4.Последовательность задана формулой  Какое из указанных чисел является членом этой последовательности? 1)31           2)30      3)28            4)29
5. Записано несколько последовательных членов геометрической прогрессии . Найдите член прогрессии обозначенной х 1)  2        2)  -2             3) 6            4)-6	5. Между числами 100 и 0,001 вставьте четыре числа, которые вместе сданными образуют геометрическую прогрессию. 1)  10; 1; 0,1; 0,01        2) -10; -1; -0,1; -0,01                 3) -10; 1; -0,1; 0,01      4) 10; -1; 0,1; -0,01

5. Поверка

1-вариант     

1	2	3	4	5
4	2	4	1	1

                

2 –вариант

1	2	3	4	5
4	3	2	2	1

 

Дополнительно :

№1. Из арифметической прогрессий, заданных формулой n-ого члена выберите ту, для которой выполняется условие а₂₇>9

1	2	3	4

 

№2 Каждой последовательности, заданной формулой n-ого члена, поставьте в соответствие верное утверждение

1) арифметическая прогрессия

2) геометрическая прогрессия

3) ни арифметическая, ни геометрическая прогрессии.

№3.Последовательность задана формулой    . Сколько членов этой последовательности больше 1?

1	2	3	4
5	4	3	2

 

№4 Выписаны первые несколько членов арифметической прогрессии: 13; 10; 7; 4;… Какое из следующих чисел есть среди членов этой прогрессии?

1	2	3	4
-3	-1	3	-2

 

№ 5. Арифметические прогрессии (х_n), (y_n), и(z_n) , заданы формулами  n-ого члена:

 х_n=8n+8, y_n=9n, и z_n=9n+9. Укажите те из них, у которых d=9

1	2	3	4
(хn), (yn), и(zn)	(хn), (yn)	(yn), и(zn)	(хn)

 

Ответы:

1	2	3	4	5
4	321	1	4	3

 

6. Задание на дом

7. Итог урока.

---